1. Overview
○ MIMO concept
MIMO(Multiple Input Multiple Output)는 무선 통신의 용량을 높이기 위한 스마트 안테나 기술이다. MIMO는 기지국과 단말기에 여러 안테나를 사용하여, 사용된 안테나 수에 비례하여 용량을 높이는 기술이다. 여기서 기지국은 송신단을 의미하고 단말기는 수신단을 의미한다. 예를 들면 기지국에 M개, 단말기에 N개를 설치할 경우 min(M,N) 만큼 평균 전송 용량이 늘어난다. 특별히 N = 1로 기지국에만 여러 개 안테나를 사용하는 경우를 MISO, M = 1로 단말기에만 여러 개 안테나를 사용 하는경우를 SIMO 그리고 (M,N) = (1,1)인 경우를 SISO라 부른다. MIMO 기술의 필요성에 대해 수신 처리 입장과 송신 처리 입장의 다른 해석이 있다. 수신 처리 입장은 간섭 제거를 중심으로한 해석이고 송신 처리 입장은 용량 증대를 중심으로 한 해석이다. 두 해석 모두 무선 통신에서 다중 안테나 기술의 중요성을 잘 반영하고 있다. 송신 처리 입장은 MIMO의 중요성을 설명하며 수신 처리 입장은 MIMO의 필요성을 설명하고 있다고 할 수 있다.

○ 수신기 입장
셀룰러 이동통신에서는 셀 간 원활한 동적인 주파수 할당을 위해서 공간 간섭의 제거가 중요하다. 뿐만 아니라 무선랜에서도 AP수의 증가로 인해 다른 AP에서 오는 공간 간섭의 처리가 중요하다. 공간 간섭의 처리 방법으로는 동적 또는 위치에 적응적으로 주파수 재사용 비율의 감소등을 이용할 수 있다. 하지만 이런 방법은 주파수 자원의 손실을 발생시킨다. 한편, 이를 다중 수신 안테나를 통해 처리하면 주파수의 손실 없이 가능하게 된다. 그러나 이런 장점에도 불구하고 단말기가 무선 간섭이 없는 위치에 가게 되면 다중 수신 안테나의 능력을 백분 발휘할 수 없다. 이를 역이용하여 무선 간섭을 발생하면서 이로 인해 다른 이득을 가져오는 방법이 있다면 전체적인 성능 향상에 도움이 될 것이다. 이에 대한 한 가지 방법이 기지국 다중 안테나 다중 스트림 전송이다. 기지국간 간섭이 존재하면 다중 수신 안테나들은 다중 기지국 공간 간섭을 제거하고, 기지국간 간섭이 없는 위치에서는 MIMO 방식으로 다중 스트림 간섭을 제거하여 용량을 증대하는 데 기여한다.
○ 송신기 입장
기지국간 또는 AP들 간의 간섭이 없는 경우에 주로 설명이 된다. 간섭이 없는 경우에는 수신 안테나의 간섭 처리 기능을 기지국의 다중 안테나 다중 스트림 전송을 통한 용량 증대에 활용할 수 있다. 이렇게 되면 기지국과 단말기에 설치된 안테나들 수 중 적은 안테나 수에 비례하여 이론적인 용량 증대가 가능해진다.
○ MIMO 용량 증대
이는 기존 통신 이론에서 다루어온 전송용량의 증가로 설명되기에는 어려움이 있다. 하지만, 다중 안테나를 통한 새로운 공간 차원을 활용하기 때문에 가능한 용량 증대라고 보면 이해하기가 쉬워진다. 기존의 통신 이론에서는 전송 용량은 사용하는 주파수와 전력에 의해서만 결정되었다. 반면, MIMO는 사용하는 기지국과 단말기의 안테나 수에 대한 새로운 관계식을 정의함으로써 용량과의 관계식을 표현할 수 있다.
다음은 정보 이론에 근거하여 SISO 환경과 MIMO 환경에서 용량 관계식을 개념적으로 정리한 것이다.
* SISO 환경에서 달성 용량
C = W log_2 (1+SNR)
* MIMO 환경에서 달성 용량 (개념식)
C = W min(M,N) log_2 (1+SNR)
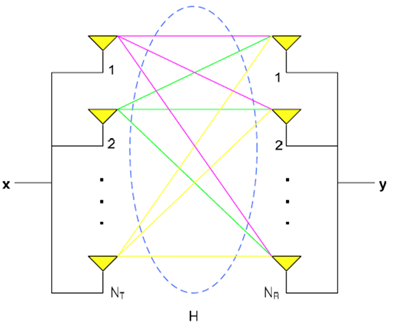
자세한 용량 관계식을 보기 전에 송수신 관계식을 먼저 보면 다음과 같다. 기지국과 단말기에 설치된 다중 안테나를 통한 단말기 수신 신호는 다음과 같다.
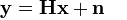
여기서 H는 MIMO의 안테나 관계에 따른 채널을 나타내는 메트릭스이다. 또한 x,y는 각각 전송신호와 수신 노이즈를 나타낸다. 이상의 관계를 통해 정보 이론으로 용량 관계식을 구해보면 다음과 같다. 먼저 기지국에서 채널 상황을 알 때인 폐루프 채널 용량이다.
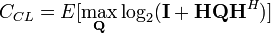
다음은 기지국에서 채널 상황을 모를 때인 개루프 채널 용량이다.
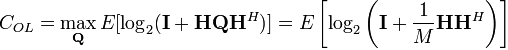
여기서 CoL에서는 Q는 1/M*I와 같은 단위 unitary matrix를 사용하면 최대화가 가능한 것이 증명되었다. 상기 두 용량 관계식은 MIMO뿐 아니라 채널 메트릭스인 H의 형태에 따라 MISO, SIMO 그리고 SISO의 경우 모두에 적용이 가능하다.
○ MIMO 통신
MIMO 통신의 발달은 우편의 그림과 같이 정리할 수 있다. MIMO 기술은 SISO 통신 기술과 방식을 계승하여 발전되어 왔으며 최근에는 새로운 통신 기술들이 그림과 같이 MIMO를 바탕으로 하여 확장되고 있다. 확장 기술은 MIMO를 확장하는 스마트 안테나 기술, MIMO의 사용을 전제로 한 통신 기술 그리고 다중 소자를 사용하여 용량을 확장하는 MIMO 개념의 확대 적용 등이 있다.
3GPP LTE (Release8), WiMAX Evolution (SDD 단계 진행)등 MIMO-OFDM 기반 이동통신 표준에서는 SU-MIMO와 MU-MIMO를 포함한 MIMO의 사용을 표준화하고 있다. 여기서 SU-MIMO는 한 사용자에게 기지국의 안테나 리소스 모두를 할당하는 방식이고 MU-MIMO는 다수의 사용자에게 안테나 리소스 또는 무선 공간 자원을 분배하는 방식이다.
○ MIMO 특징
MIMO의 특징은 3가지로 규정지을 수 있다. 첫째. 주파수 효율성 측면이다. 무선 데이터의 용량이 증가하고 고속 데이터 전송이 가능해 진다. 두 번째 데이터 전송 속도 측면이다. 이는 동일 채널로 전송되는 서로 다른 데이터 스트림 수에 정비례해서 증가하게 된다. 마지막으로는 다차원적 신호 측면이다. 여러개의 신호들이 각각 서로 다른 무선 장치와 안테나로부터 전송 가능하다.
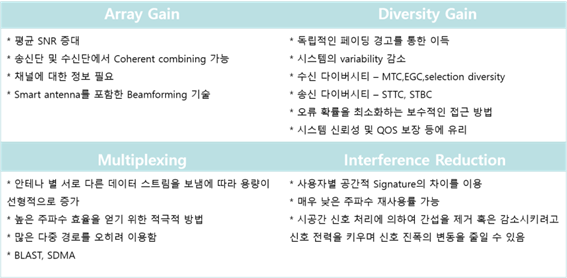
○ Array Gain(Coding Gain)
Coherent 수신 신호를 합성하여 얻어지는 평균 수신 SNR이 증가한다. 이 뿐 아니라 Transmitter/Receiver에서 채널 정보를 알아야 한다.

Full array gain을 얻기 위해서, 하나의 채널 Maximum eigenmode를 송신해야 한다.
Nx1과 Mx1 배열에서, Array gain은 10log10N 과 10log10M dB로 나타난다.
○ Diversity Gain
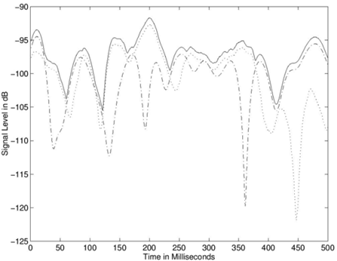
페이딩에 대처하기 위해서 주어진 신호의 동일한 사본 여러 개를 수신기에 제공한다. 이는 순간 SNR 이득이다.
직관적으로, 수신기가 제공되고 주어진 신호보다 독립 페이딩, 동일한 복사본은 빠른 BER은 SNR의 함수로써 감소한다.
높은 SNR값으로 아래와 같이 나타난다.
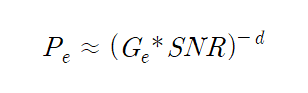
여기서 d가 나타내는 값이 Diversity gain이고 Gc가 나타내는 값이 Coding Gain 이다. Transmission Rate R이 주어 졌을 때, Diversity gain은 아래의 식으로 구할 수 있다.


○ Multiplexing Gain
Throughput을 증가시키기 위해 각각의 안테나가 서로 다른 정보를 전송하는 것이다.
○ 샤논의 한계
샤논의 정리가 나타내듯이 신호 전송 채널의 채널 용량 C는 신호/잡음과 채널 대역폭 B로 정해진다. 그러나 무잡음 선로에서는 C가 무한대가 된다. 그러나 B가 넓어져도 그에 따라서 잡음이 증대하기 때문에 CD에는 일정한 한계가 있다.

○ Co-channel Interference
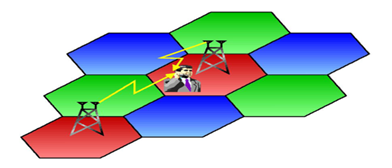
주파수가 같은 동일 채널의 둘 또는 그 이상의 전파가 수신기에 간섭하여 장애를 일으키는 현상을 일컫는다. 동일 채널 혼신이라고도 한다. 이것을 막기 위해 동일 채널 무선국의 간격, 공중선 전력, 안테나 패턴 및 순차적 전송 등을 고려해야 하지만 전파의 이상전파 또는 이상반파로 인해 예상외로 먼 지점에서 간섭을 일으키는 경우도 있다. 동일한 주파수의 파동이 합성 될 때, 동 위상인 경우는 더해지고, 역 위상인 경우에는 상쇄되는 현상을 전파의 간섭현상이라고 한다. 이동통신에서의 간섭은 3가지로 나누어진다. 첫째, 시간차에 의한 간섭. 이는 동일 주파수이고, 동일한 기지국에서 방사된 전파가 여러 경로를 거치면서 전파의 도달 시간 차이에 의해 발행한다. 둘째, 동일 채널 간섭. 이는 다른 기지국으로부터 방사되는 동일 주파수에 의한 것이다. 셋째 인접 채널 간섭. 이는 인접하는 주파수 채널에 의한 영향으로 발생한다. 특히 CDMA 이동통신에서는 동일 채널 간섭에 의한 영향이 지배적이다. 동일 채널 간섭 영향은 CDMA 방식은 인접 기지국 간에 동일한 주파수를 사용하므로 기지국 간 간섭으로 통화 품질에 영향을 준다. 제한된 장소에서 기지국 수가 많을수록 가입자를 더 많이 수용할 수 있지만, 동일 채널 간섭으로 Qos에 영향을 주므로, 가입자가 증가함에 따라 다른 주파수를 하용하게 된다. 어떤 기지국의 인근 지역이 호수와 같은 넓은 수면환경이라면, 주파수 재사용으로 인해 인근 기지국으로부터 동일 채널간섭현상이 증가하여 CDMA 용량에도 영향을 미친다. 가입자의 입장에서 보면 특정 가입자가 기지국과 통신할 경우, 그 기지국과 통신하는 나머지 가입자는 모두 Interference이다.
이에 대한 대책으로는 사용 주파수를 확대하는 방법과 기지국을 세분화, 섹터 분할 방법 그리고 최적 전파 환경을 구축하는 방법과 마지막으로 순방향, 역방향 전력을 제어하는 방법이 있다.
결국 이동통신의 경우, 일반적으로 다른 무선 통신보다 기지국 출력이 작으므로 특정 기지국에서 사용한 주파수를 다른 기지국에서 재사용하여야 하고, 재사용율이 높을수록 가입자 수용률은 증가하나, 동일 채널간 간섭으로 통화 품질에 영향을 준다. CDMA의 경우, 모든 기지국이 같은 주파수를 사용하므로 동일 채널 간섭이 더욱 무제가 되며, 이에 대한 방지책으로써 가입자가 많아질수록 주파수를 확대하여야 하고, 기지국을 더 세분화하여 3 섹터로 구분하여 서비스를 하여야 한다.
또한 순방향 전력제어에 의해 기지국의 송신전력을 되도록 줄인다.
IS-95 시스템에서 무선 구간 용량은 역방향 채널이 더 결정적으로 작용하며, 특정 가입자가 기지국과 통신할 때 나머지 가입자는 모두 간섭으로 작용하므로, 최적의 전력제어와 전파 환경 구축이 요구 된다. 동일 채널 간섭을 줄이기 위해서는 Directional 안테나를 Base station에서 사용하거나 Base Station에서 안테나의 높이를 낮추는 방법이 있다.

SISO(Single Input single Output)은 한 개의 송/수신 Antenna를 사용한다.
SIMO(Single Input Multiple Output)은 한 개의 송신 안테나와 여러 개의 수신 안테나를 사용한다. MISO(Multiple Input Single Output)은 여러 개의 송신 안테나와 한 개의 수신 안테나를 사용한다.

MIMO는 여러개의 송/수신 안테나를 사용한다 (Transimit antenna : N_T, Receive antenna : N_R) 여기서 Diversity Gain은 N_T * N_R로 나타낼 수 있고 Capacity는 min(N_T,N_R)로 나타낼 수 있다.
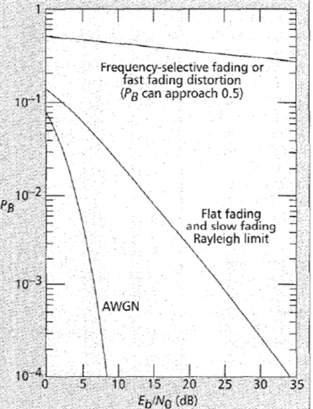
○ Fading effect
만약 잡음만 존재하는 환경이라면 신호 전력을 높임에 따라 BER이 빠르게 떨어진다. 그리고 신호 전력을 높임에 따라 BER이 줄어들기는 하지만 AWGN보다는 SNR이 더 필요하다. 그리고 Frequency Selective Fading에서는 Fading의 영향이 심각하여 통신이 불가하다. 이를 해결 하는 방법이 바로 Diversity이다.
○ 사용자 별 채널 할당
- Single user MIMO
두개의 스트림은 채널 상태의 최상 조합을 위해 혼합한다. 그리고 2*2 SU-MIMO에서 DownLink는 의무 사항이고, UpLink는 옵션 사항이다.

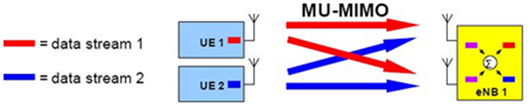
- Multi user MIMO
각기 다른 UE로부터 데이터 스트림이 전달된다. 여기서 셀 Capacity는 증가하지만 단일 유저의 data rate는 증가하지 않는다.
2. MIMO Diversity Concept
○ 다수의 안테나에서 같은 데이터를 보내는 기술이다.

○ Time Diversity
이동 통신 시스템에서 사용되는 다이버시티 기법에는 시간 다이버시티가 있다. 시간 다이버시티는 레이크 수신기를 이용하는 방법으로 앞에서 설명했듯이 다중경로마다 페이딩 특성이 서로 다르기 때문에 각 다중 경로 신호의 시간 지연을 보상한 후 합성하여 페이딩이 적은 신호로 만들 수 있다. 특히 각 다중 경로 신호의 시간 지연차가 클 경우에 시간 다이버시티를 이용하지 않을 경우에 ISI가 발생하므로 이러한 시간 다이버시티는 페이딩이 적은 신호를 만들어 내는 다이버시티의 효능 이 상의 이동통신 시스템의 성능 향상 효과가 있다.
이를 자세하게 설명하자면, 시간축상에서 각기 다르게 전송된 신호의 복제본을 페이딩 영향이 적도록 합성하여 수신 처리하는 방법으로써 송수신간에 나타나는 Multi path마다 페이딩 특성이 서로 다르기 때문에 각 multipath 신호의 시간지연을 보상 합성하는 등 페이딩이 적은 신호로 만드는 방법이다.
채널의 상관시간(Coherence Time)보다 긴 시간간격으로 정보 전송, 각각 독립적인 페이딩 환경을 겪게 되는 여러 다중경로 수신 신호를 합성한다.
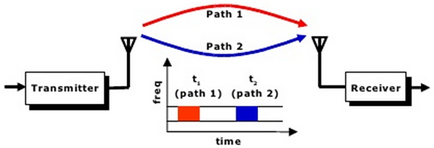
○ Frequency Diversity
주파수 다이버시티 기법은 주파수마다 서로 다른 전파 특성을 가지므로 서로 페이딩 특성이 독립적인 두 개 이상의 주파수를 동시에 사용하는 다이버시티 기법이다. 독립적인 페이딩 특성을 가질 수 있는 주파수 간격은 주파수 밴드별로 다른데 보통 10MHz 정도 이다. 보다 넓은 의미에서의 주파수 다이버시티 기법은 다중반송파 시스템뿐만 아니라 frequency - hopping 시스템도 포함한다.
현재 이동통신 시스템의 기지국에서 많이 사용되어지는 다이버시티 기법은 공간 다이버시티 기법이다. 앞으로는 편파 다이버시티 기법을 이용한 안테나와 같이 기존의 시스템 성능을 증가시키면서도 기존의 안테나와 비교 소형, 경량화 시킬 수 있는 안테나에 대한 연구가 이루어져야 할 것이다.
이는 주파수 상에서 다이버시티 효과를 얻고자 하는 기법으로 주파수가 다른 2 이상의 동일 정보신호 전송을 했을 때, 수신측에서 2 이상의 신호 중 양호한 신호를 선택 또는 합성하여 수신하는 것이다.
이의 구현 원리는 서로 떨어진 주파수의 반송파를 이용하여 정보신호를 보내서 서로 다른 전파특성에 따라 동시에 레벨 저하가 생길 수 있는 기회가 적어지므로 다이버시티 효과가 얻어진다. 이는 복수의 주파수를 사용하여 주파수 이용효율을 저하시키고 넓은 주파수대역폭을 사용해 신호 확산을 하여 확산대역 내 주파수 다이버시티 효과를 주는 것이다.

○ Space Diversity
이동통신 시스템에서 사용되는 공간, 편파, 시간 그리고 주파수 다이버시티도 사이트 다이버시티와 같은 견지에서 이해할 수 있다. 공간 다이버시티는 2개의 수신안테나를 공간상으로 이격시키는 방법으로 이격 거리는 보통 10~20 λ 이다. 서로가 이격된 안테나로부터 수신되는 신호들은 서로 다른 위상 변화를 겪기 때문에 각각 서로에 대한 낮은 상관성을 가지게 된다. 여기에서 낮은 상관 특성을 가진다는 것은 한쪽 신호와 다른 쪽 신호의 다중경로 페이딩 특성이 서로 독립적임을 의미한다. 그러므로 한 신호가 깊은 페이딩에 빠질 때 다른 신호는 깊은 페이딩에 빠질 확률이 적게 되며 이러한 두 신호를 합성하면 다중경로 페이딩이 적은 신호로 만들 수 있게 된다.

이는 송수신 기지국 등에서 여러 다중 안테나를 두고, 서로 다른 무선 채널을 통과한 신호를 수신하고 이중에 페이딩 영향이 적은 것을 취사 선택하거나, 합성하여 수신, Space Diversity는 여분의 대역폭 및 송신 전력 없이 다이버시티 효과를 볼 수 있다.

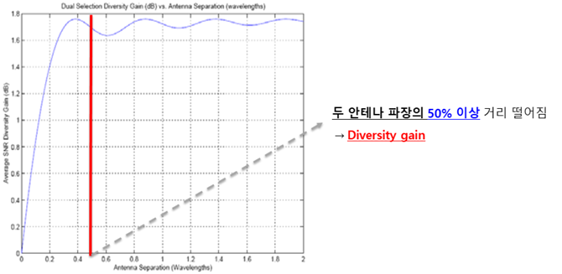
위에서 이야기 했듯이, 안테나 간의 상관도가 낮으면, 다이버시티 이득이 증가하게 된다. 즉 안테나 간의 상관도와 다이버시티 이득은 반비례 관계에 있다고 할 수 있다. 하지만 안테나간의 상관도가 1이면, 즉 두 안테나의 특상관관계가 거의 같으면, 다이버시티 이득은 없다고 볼 수 있다. 두 안테나 사이의 이격 즉 둘 사이의 거리의 격차가 없으면 다이버시티 이득이 없다. 하지만 두 안테나 사이에 파장의 50% 이상의 거리가 이격 되어 있다면 다이버시티 이득이 있음을 우측의 표를 통해 확인할 수 있다.
○ Receive Antenna Diversity
수신단에 다중 안테나를 사용하여 다이버시티 효과를 내도록 한 기술로써 과거부터 사용되던 방식이다. 예를 들면 IS-95의 역방향 링크에서부터 사용하였다. 여러 가지 안테나를 사용한다는 것은 다이버시티 이득이 증가한다는 것이고, 안테나를 추가하면서 늘어나는 이득의 양은 줄기 때문에 결국 이득의 증가가 한계에 부딪힌다.
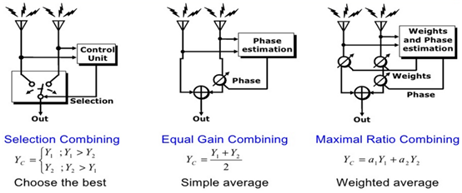
Receive Antenna Diversity의 방식에는 SC, EGC, MRC 등의 방식이 있다.
○ SC(selection Combining)
이 방법은 복수개의 안테나를 통해 수신된 두 신호들 중에서 더 우수한 품질(예를 들어 더 높은 RSSI 혹은 더 높은 SNR)을 나타내는 한 신호만을 골라서 그 신호를 이용하여 신호를 복조하는 방법이다. 따라서 양쪽 안테나 모두가 deep fading에 빠져있을 확률은 안테나 하나가 deep fading에 빠져 있을 확률보다 상대적으로 낮기 때문에 다이버시티를 사용하지 않은 시스템에 비하여 좋은 성능을 얻을 수 있다. 또한 RF 및 아날로그 소자들은 복수 개를 사용하지만, 일단 RF 대역 혹은 아날로그 영역에서 그 중 한 신호만을 선택하여 처리하므로 기저대역 디지털 영역에서는 복수 개의 수신 경로가 필요하지 않게 된다.
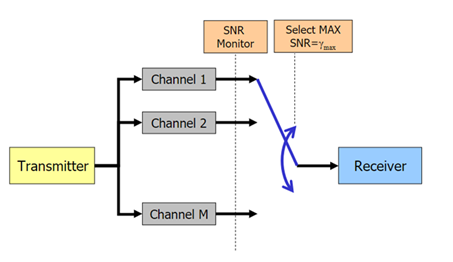

○ MRC
두 개의 안테나로 수신된 신호에 대하여 간단한 equl gain combining 보다 더 우수한 수신 성능을 얻기 위한 방법으로써 MRC방식이 제시되었다. MRC방식은 두 개의 수신 안테나를 사용하여 수신 SNR이 최대가 될 수 있도록 동작한다.

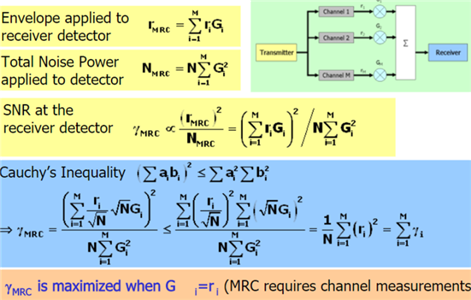
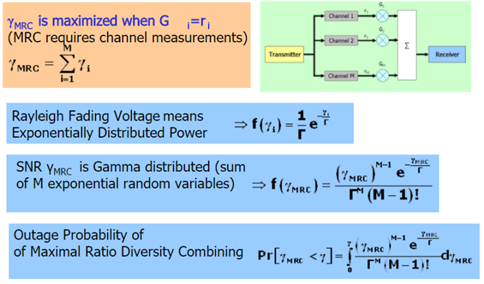
○ 수신 안테나의 MRC 방법
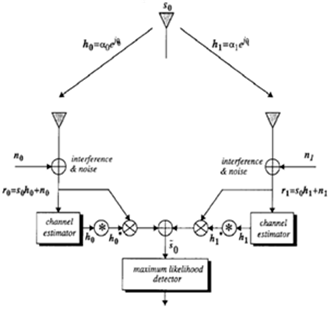
두 개의 안테나에서 수신된 신호를 각각 r0, r1이라고 하자, 여기서 s0는 송신된 동일한 데이터 신호이며 n0,n1은 두 수신 안테나 단에 더해지는 잡음 및 간섭 부분이 된다. h0와 h1은 송신 안테나와 두 수신 안테나 사이의 채널을 나타낸다.
이 두 수신 신호를 어떻게 결합할까? 각 수신 신호에 각 채널의 conjugate를 곱하여 합해주는 것이다. 즉 conjugate를 곱함으로써 각 채널을 통화하면서 생긴 위상의 변화를 보상해줌, 각 채널의 신호 크기로 weight를 가해줌으로써 더 품질이 좋은 경로 신호에 더 많은 중요도를 주는 것이다.
○ 송신 안테나의 STC 방법송신 다이버시티 수식은, 완전한 다이버시티 이득을 얻기 위해서는 안테나 상의 프로세싱 뿐만이 아니라 시간 상의 프로세싱이 병행되어야 한다는 발견에서 비롯되었으며, 따라서 시공간부호화라고도 한다. 송신 다이버시티 수식에는 제안자의 이름이 붙여져서 Alamouti 코드라고 불리게 되었다.
○ 기존의 수신 MRC와 매우 유사한 구조임을 알 수 있다. 한 심볼 구간 동안에 두 개의 안테나로 각각 서로 다른 두 심볼 s0와 s1을 보내주는 것으로 보일수도 있으나, 연속된 두 심볼 구간을 살펴보면 결국 두 심볼 주기에 두 심볼을 보내주는 것이므로 앞의 수신단 안테나 다이버시티의 경우와 주파수 효율은 동일한 것을 알 수 있다. 이 때, 아래와 같이 두 심볼 주기동안의 채널 특성은 변하지 않는다는 것을 가정한다.
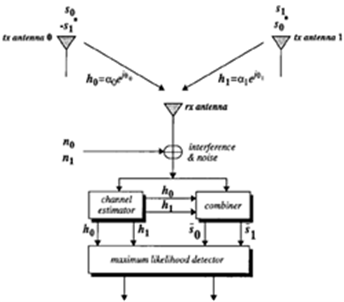
○ Alamouti code
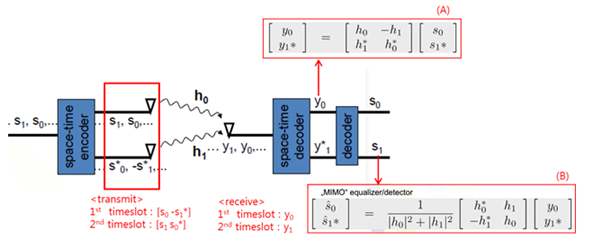
2개의 송신 안테나를 이용하며 다음과 같이 동작.
1. transmitter의 첫 번째 안테나는 s0, 두 번째 안테나는 -s1*을 동시에 전송한다.
2. receiver는 해당 data를 수신한다.
3. transmitter의 첫 번째 안테나는 s1, 두 번째 안테나는 s0*을 동시에 전송한다.
4. receiver는 해당 data를 수신한다. 이때 y0와 y1은 s0와 s1과 (A)같은 관계에 있다.
5. receiver의 MIMO equalizer는 (B)식을 활용하여 s0와 s1을 추출한다. 이때 필요한 것은 채널정보 h0와 h1이며 receiver는 해당 channel의 정보를 이미 보유하고 있으므로 쉽게 구현이 가능하다. Alamouti code는 채널 정보를 이용하기는 하지만, receiver단의 equalizer에서 필요하다. 즉 채널정보를 transmitter로 보낼 필요가 없으므로, Open-Loop MIMO이다. 또한 2개의 안테나에 대해 복소 직교 설계를 이용한 송신 다이버시티 기법으로 총 전력이 2개의 송신경로로 나뉘어져서 각 경로는 3dB 낮은 송신전력을 가진다.

* BER of MRC&STC
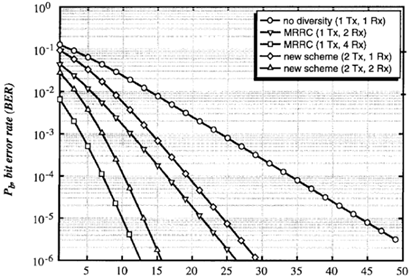
○ Transmit Antenna Diversity
2세대 이동통신 시스템에 비하여 3세대 그리고 이후의 세대에서의 송,수신 통화유형을 추측하면 하향링크로 데이터 전송량이 몰리는 비대칭적인 전송형태를 보일 것으로 예상된다. 따라서 하향링크에서의 전송속도와 용량이 상향링크에 비해 더욱 강조되어야 함을 알 수 있으며, 이를 위하여 하향링크 송신 다이버시티 기능이 강조되고 있다. 구현이 간단하고 이득이 높은(2~7dB) 수신 안테나 다이버시티에 비하여 송신 안테나 다이버시티는 상대적으로 구현 비용이 높고 얻을 수 있는 이득은 1~2dB 이내로 낮다. 따라서 수신 안테나 다이버시티는 선택적인 사항으로 채택되고 있다. 송신 다이버시티 기법은 동기식 진영에서 제안되었던 OTD 방식과 비동기식 진영에서 제안된 STTD방식으로 크게 분류된다. 비동기식 3GPP 진영의 송신 안테나 다이버시티는 피드백 정보가 필요 없는 개루프 방식인 STTD와 단말기로부터 피드백 정보를 수신하는 폐루프 송신 안테나 다이버시티 방식으로 나뉘게 된다. 송신 안테나 다이버시티의 정확한 이론적 수식은 수신 안테나 다이버시티의 식이 1959년에야 발표된 것과 비교하여 많은 시간이 지난 1998년에야 Alamouti에 의해 확립되었다.
이는 쉽게 말해 송신단에서 다중 안테나를 사용하여 수신 다이버시티 효과를 낸 기술로써 단말기 측의 크기, 전력, 비용의 한계가 있어 송신단에만 다중 안테나를 사용한다. DownLink에 많은 데이터가 보내지는 비대칭형 전송에 유리하다.
송신 안테나 다이버시티의 기법으로는 Open Loop Transmit Diversity 와 Close Loop Transmit Diversity가 있다.
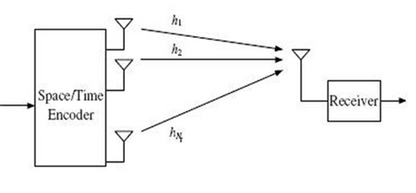
○ Open loop transmit diversity
Transmitter와 receiver간 Channel 정보는 receiver의 경우 channel estimation을 위해 미리 정의된 pilot signal이 있기 때문에 쉽게 알 수 있다. 하지만 transmitter는 해당 channel 정보를 일반적으로 알 수가 없다. 이러한 system을 open-loop 라고 한다. Open loop transmit diversity의 방식으로는 OTD, TSTD, STTD, Double-STTD 등이 있다.
○ OTD(Orthogonal Transmit Diversity)
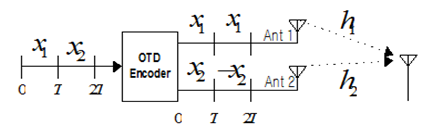
데이터 값에 서로 다른 Wash code를 사용해 다중 안테나로 전송하는 방식이다. 이 방식에서는 두 개의 안테나에 서로 다른 직교 코드를 곱하여 전송하여 두 방식을 구분한다. 여기서 수신신호는
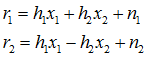
이고, OTD Decoding 된 신호는

이다. 이는 송신 데이터 심볼의 추정치를 얻게 된다.
○ TSTD(Time Switched Transmit Diversity)

이 방식은 송신 안테나를 번갈아가면서 사용하는 형식을 사용한다. 안테나 1은 홀수번 slot에 x1, 안테나2는 홀수번 slot에 x2를 전송하게 된다. 송신측에서는 이러한 방식을 사용하고, 수신측에서는 시간의 차이를 이용하여 신호를 다시 결합하게 된다.
이 방식은 STTD를 확장한 개루프 방식으로 송신 안테나가 4개로 구성된다. 2개의 송신 안테나를 묶어 하나의 STTD 인코더로 사용하기 때문에 결국 송신기에는 2개의 STTD 인코더가 존재한다. 여기서 입력 데이터 스트림은 2개의 스트림으로 나눠 각각의 STTD 인코더에 의해 인코딩 되어서 전송 되어 진다.
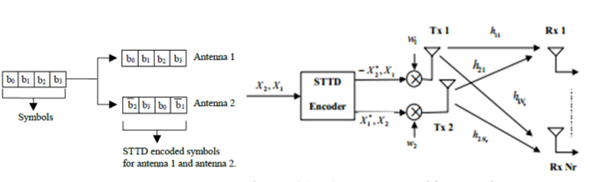
○ Double-STTD(Double Space Time Transmit Diversity)
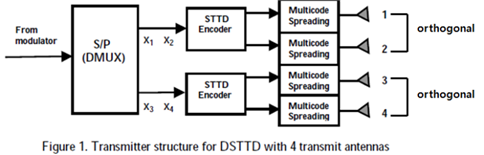
이 방식은 STTD를 확장한 개루프 방식으로 송신 안테나가 4개로 구성된다. 2개의 송신 안테나를 묶어 하나의 STTD 인코더로 사용하기 때문에 결국 송신기에는 2개의 STTD 인코더가 존재한다. 여기서 입력 데이터 스트림은 2개의 스트림으로 나눠 각각의 STTD 인코더에 의해 인코딩 되어서 전송 되어 진다
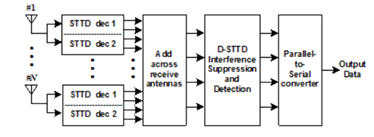
수신단 에서는 수신 안테나 수가 N개이고 2개의 STTD Decoder를 통해 전송된 신호를 decoding 하게 된다. 모든 출력은 더해진 후 iterative MMSE 방식과 같은 알고리즘으로 간섭을 줄이기 위해 신호 처리를 하게 된다. 송신기에서 같은 STTD Encoder를 거친 전송신호들은 orthogonal 하지만, 서로 다른 STTD Encoder를 거친 신호들 간에는 간섭을 일으킨다.
○ Closed loop transmit diversity
만약 수신단으로부터의 적절한 피드백에 의하여 송신단이 중간에 존재하는 무선채널을 좀 더 잘 알 수 있다면, 보다나은 MIMO동작이 가능할 수 있다.
○ TxAA(Transmit Antenna Array)
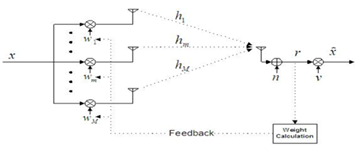
수신 안테나가 하나일 경우에 대한 전송 빔형성 시스템이다. 수신기에서 채널의 상태를 측정하여 채널 상태에 따른 최적의 송신 가중치를 계산 후 이를 송신기로 귀환시키며 이 값을 송신 신호에 곱하여 송신하여 다이버시티를 얻는다.
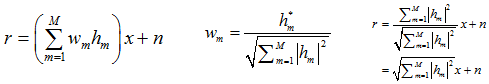
○ Basis selection
송신단에서 데이터 스트림을 전송하기 유리한 안테나 조합 정보를 사용하는 기법으로써 수신단에서 채널 상태 정보에 기반한 연산결과를 귀환하여 얻어진다. 이는 피드백 정보량을 줄이는 방법으로써 사용되고 있다.
○ Eigen-Beamformer
송신 안테나 증가에 따른 feedback 정보량을 줄이기 위해 제안된 방식으로써 송신 안테나 간 채널의 상관관계가 높도록 하기 위해 간격을 작은 시스템이라고 가정한다.
UE에서 파일럿 채널로 채널 정보를 구하고, 공간 상관 행렬을 구한 후, 고유 벡터를 구한 후에 기지국으로 Feedback 해준다.
3. MIMO Multiplexing Concept
가. MIMO multiplexing
○ MIMO SM
CDMA 기술이 한창 성장하던 1990년 초반에, 아주 각광 받았던 기술 중에 다중사용자 검출과 다중반송파 시스템이 있었다. 차세대 이동통신 기술이 점차 CDMA 기반에서 OFDM으로 옮겨가고 있는 최근의 추세로 볼 때, multi-carrier 시스템이 추구하던 일부 목표는 OFDM에 흡수가 되었으며 multi-user detection의 경우는 그 신호 처리의 기본 이론이 MIMO와 유사하므로 MIMO 수신기에도 여전히 적용되고 있으며 차세대 이동통신에서의 간섭 제거 기법 등으로 응용되어 연구되고 있다. 이와 함께 2000년을 넘어서면서, WiFi 표준을 제정한 IEEE 802.11 working group에서 가장 먼저 논의가 시작된 Multiple Input Multiple Output(MIMO) 라는 기술이 각광을 받고 있다. 이 기술은 이미 802.11n 표준에 채택되어 2007년 9월 현재 이미 시장에서 802.11n 기반의 제품을 찾아볼 수 있으며, IEEE 802.16의 mobile WiMAX 기술에도 채택되어 2008년도 중반부터는 MIMO가 적용된 mobile WiMAX가 상용망에 적용되고 있다. 아울러 이 기술은 3GPP LTE에도 고려되고 있으며, 여러 회사에서 4G의 시험 시스템 발표 시마다 어김없이 MIMO 기술을 포함시키고 있다. 유한한 주파수 자원과 기지국 국소확보의 어려움을 고려한다면, 더 높은 데이터 속도를 달성하기 위하여 더 높은 주파수 효율성의 통신 기술을 개발하여야 하며, 이러한 기술적 요구를 만족시키기 위하여 MIMO 기술이 등장하게 되었다.
< MIMO SM의 기본 개념 >
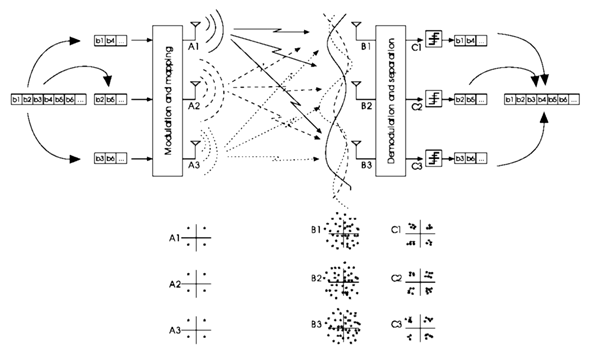
무선 구간에서 반사파에 의한 다중 반사파 현상은 통신 시스템의 수신 성능을 저하시키는 주요한 요인이기도 하지만, CDMA 시스템의 RAKE 수신기에서는 이러한 다중 반사파를 잘 이용하여 합치면 수신 신호에서 다중 반사파 다이버시티 이득을 얻을 수 있다는 것을 알 수 있었다. 이러한 다중 반사파 현상을 조금만 더 잘 이용하면 주파수 효율을 N 배 까지 올릴 수 있는데, 이 기술 방식이 바로 MIMO시스템이다. MIMO라는 이름과 아래 그림을 살펴보면 송신 측과 수신 측에 모두 복수 개의 안테나를 사용하여 시스템의 성능 향상을 꾀하는 방식이다.
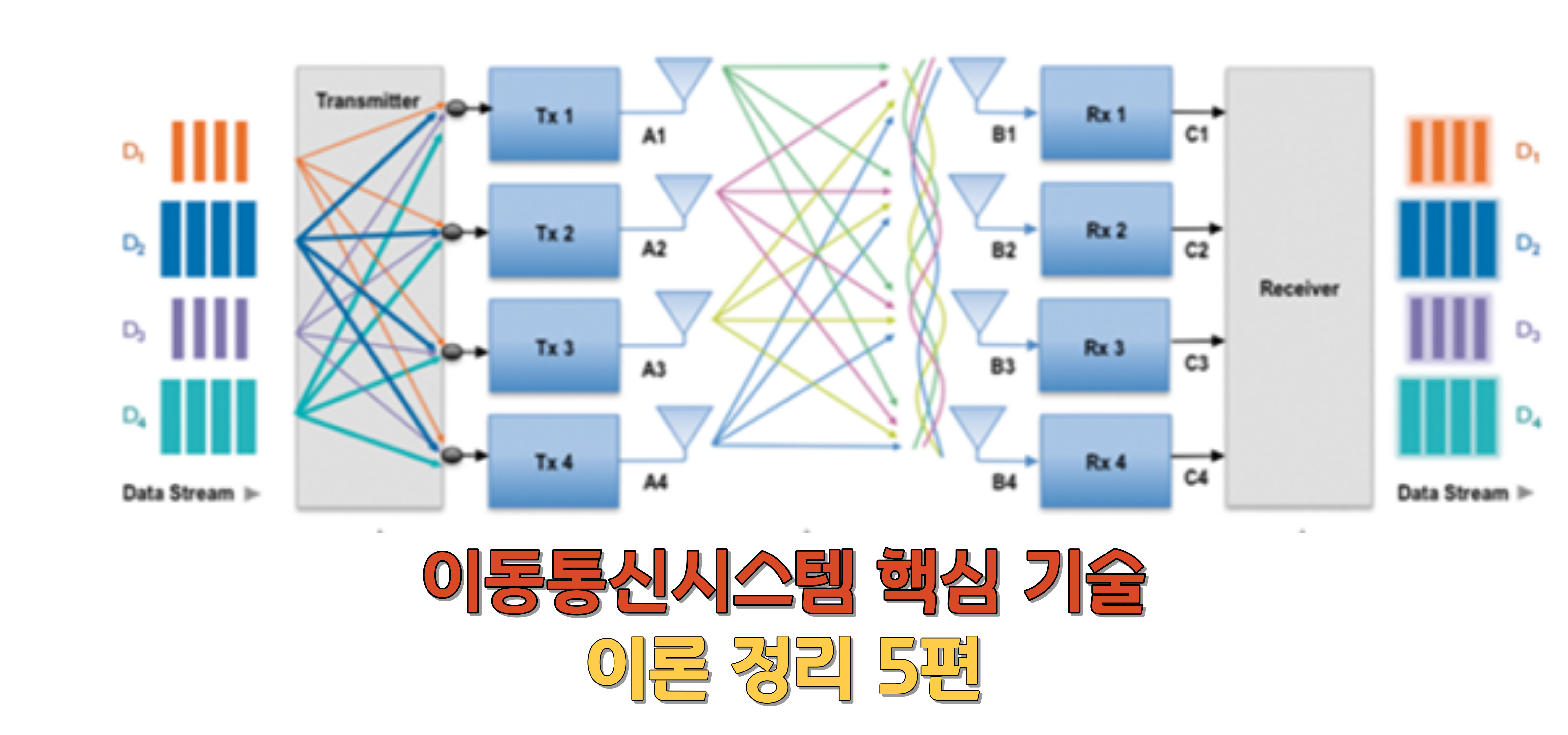
(Throughput 증가 시키기 위해 각각의 안테나가 서로 다른 정보를 전송)
MIMO Multiplexing에서 single user와 Multi-User인 경우를 살펴보자.
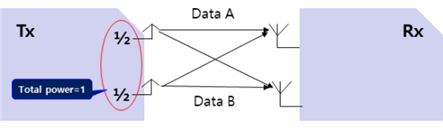

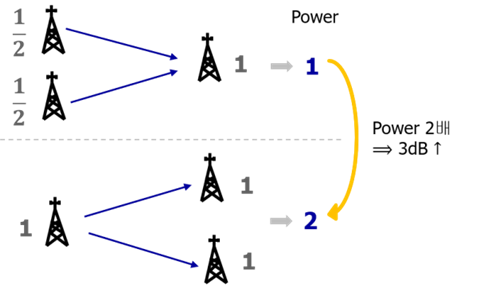
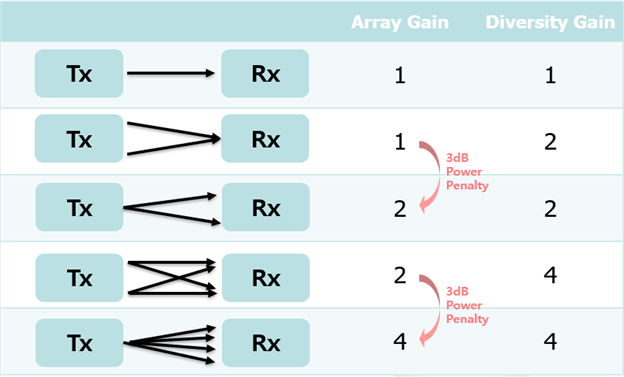
위에 그림은 Single User일 때 Tx와 Rx의 서로 다른 데이터를 전송할 때의 Array Gain과 Diversity Gain을 살펴 본 경우이다. Tx에서 전송 하는 전체 파워는 1로 Rx의 각각의 안테나에 받아서 A data와 B data는 각각 Array Gain은 1이며 Diversity Gain은 받는 data가 수신단에 각각2개 이므로 각각의 값은 2가 된다.
다음 그림은 multi-User일 때 서로 다른 데이터를 전송 할 경우를 살펴 본 것이다. A data를 보내는 Tx와 B data를 보내는 Tx가 따로 존재 하게 되므로 각각 power를 1로 사용해 총 power는 2를 사용해 보내게 된다. 따라서 수신 단에서 Array Gain은 2가 되며 수신단 Rx에서는 서로 다른 data 수신함으로써 각각의 interference가 존재하게 된다. 수신단에 각각 두 data를 받음으로써 Diversity Gain은 4가 된다.
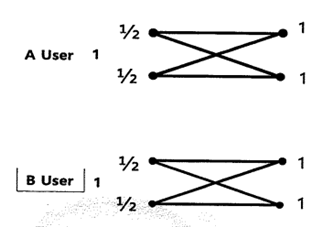
복수개의 안테나를 사용하여 얻을 수 있는 Gain을 위해서 간단하게 살펴보았다. 이러한 복수 개 안테나를 사용하여 얻을 수 있는 Gain들의 특징은 다음과 같다.
이러한 시스템을 다음과 같이 살펴 볼 수도 있다. 간단하게 송신측에 안테나가 2개, 수신측에 안테나가 2개 있는 2*2 시스템을 생각해보자. 이 경우에, 송신 안테나 1번과 수신 안테나 1번 사이의 채널 특성을 h11, 송신 안테나 1번과 수신 안테나 2번 사이의 채널의 특성을 h12, 송신 안테나 2번과 수신 안테나 1번 사이의 채널 특성을 h21, 송신 안테나 2번과 수신 안테나 2번 사이의 채널 특성을 h22라고 하자. 이 경우의 채널 특성들을 한데 모으면 아래와 같은 행렬이 만들어진다.

따라서 2개의 수신 안테나에 수신되는 신호 는 다음과 같이 표시될 수 있다.
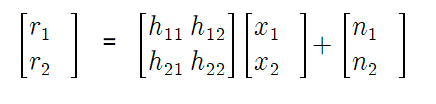
이때 x1, x2는 각각 송신 안테나 1과 2에서 송신되는 신호가 되며, n1과 n2는
각각 수신 안테나 1과 2에 존재하는 잡음이 된다.위의 기초적인 수식을 토대로 다음의 2가지 예를 살펴보자. 행렬의 예를 분석하면 5=1x1 + 2x2 와 10=2x1 + 4x2로 두식은 정보량이 하나인 결국 같은 식임을 알 수 잇다. 반면에 다른 행렬은 두 개의 식이 다른 식이므로 결국 행렬 혹은 연립 방정식을 풀면 서로 다른 송신신호 x1과 x2의 값을 구해낼 수 있다. 수신단에서 수신신호 와 채널 특성을 토대로 서로 다른 안테나를 통해 전달된 서로 다른 송신신호 x1, x2를 구해낼 수 있다는 말은, 바로 복수개의 안테나를 통해 서로 다른 데이터를 mux해서 보내는 spatial multiplexing 시스템이 가능하다는 이야기이다. 왼쪽의 5와 10은 수신신호에 해당하며, 오른쪽의 x1과 x2는 송신신호에 해당하며 2*2행렬은 송.수신 신호간의 무선 채널과 안테나의 구성에 의한 전달함수가 된다. 무선 구간에서 전달특성이 서로 다른 다양한 반사파가 아닌 직접파 위주의 전달 특성에 의하여 만들어진다면, 송신과 수신 안테나 각각 사이의 채널이 비슷한 특성을 띄게 되므로 위의 식과 같은 채널 행렬이 만들어 진다. 이 경우, 채널 행렬이 가진 정보랴은 1에 해당하며, 즉 비록 송수신 양쪽에 2개씩 안테나를 사용하였더라도 동시에 2개의 서로 다른 데이터를 전달할 수가 없게 된다. 반대로 무선채널상의 서로 다른 다양한 반사파에 의하여 각 안테나 사이의 채널 특성이 서로 달라서 채널 행렬이 위와 같은 형태를 띠고, 수신기 측에서 이 행렬을 정확하게 풀어낼 수만 있다면 송신 측과 수신 측에 2개의 안테나를 사용함으로써 동시에 2개의 서로 다른 정보를 보낼 수 있게 되어 정보 전송 능력이 2배로 증가하게 되는 것이다. 즉 같은 주파수, 같은 공간, 같은 시간을 사용하면서, 다중 안테나를 통하여 각기 다른 정보를 전송할 수 있게 됨으로써 정보 전송 능력을 높이게 되는 것이다. 이를 MIMO spatial multiplexing 방식 이라고 한다. 이 기술을 통해서 대량 고속화 다중화가 가능하게 된다. 지금 까지 방해요소라고만 알고 있었던 다중 반사파가 어떤 경우에는 오히려 주파수 효율을 몇 배 올려줄 수도 있으니, MIMO기술은 실로 엄청난 기술이 아닐 수 없다.
4. D-BLAST, V-BLAST, Turbo-BLAST
가. D-BLAST, V-BLAST, Turbo-BLAST
○ 원래는 1996년 Foschini에 의해 제안된 이 구조는 Shannon 한계에 가까운 용량을 도달 할 수 있으므로 MIMO 시스템의 성능을 기준으로 간주된다. 그러나 복잡성은 아직 실제적으로 너무 높다. 레이어의 데이터가 공간 및 시간 축 상에서 대각선으로 전송되는 것처럼 보여 대각선 layering에 해당하는 시공간 배치를 사용한다. 일정 시간에 상응하는 차를 두고 안테나를 이동시키면서 전송하면 된다. 디코더의 구조에 따라 공간 시간 소모가 필요하며 새로운 집합의 layer가 전송될 때마다 시공간적 소모가 발생한다. Symbol이 여러 안테나를 통해 전파되므로 이 방식이 효과적이다. 또한 채널 용량 측면에서는 약 90% Shannon 용량에 도달한다.
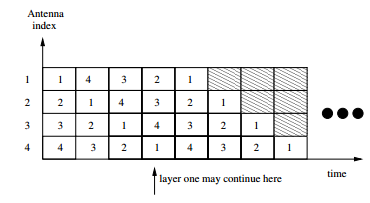 [ D-BLAST ] |
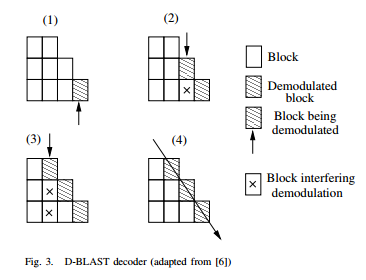 [ D-BLAST Decoder ] |
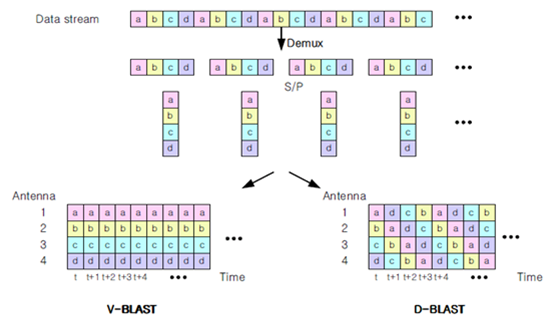
나. V-BLAST
○ 서로 다른 신호가 전송된 여러 안테나 layer 중에서 우선 가장 신뢰성 있게 수신될 것으로 여겨지는 층의 신호부터 검출을 한다. 검출된 신호는 최초 수신 신호에서 제거하고 다시 그 중에서 가장 신뢰성 있는 신호를 검출한다. 이와 같은 작업을 전체 층의 신호가 모두 검출될 때까지 반복한다. 기존의 D-BLAST 구조의 복잡도를 줄이며 각 레이어의 데이터가 고유의 송신 안테나로 전송되어 공간과 시간 축 상에서 수직한 형태를 갖는다. 단일 송신 안테나 일 때 보다 송신단에서 M개의 안테나를 사용해 전송률이 N배 증가하는데 안테나의 수가 증가해야하는 제한이 생기게 된다. 이러한 방법을 통해 수신기에 신호가 전달이 되면 다음과 같은 검출 과정을 따른다.
- Detection ordering : 검출 순서를 정하는 과정, 각 검출단계마다 가장 큰 SNR을
갖는 Symbol을 선택하여 검출하는 방식
- Interference nulling : 어느 한 전송신호를 검출해 내기 위해 나머지 전송신호들을 nulling시키기 위한 적절한 가중치 벡터를 수신 신호 벡터에 곱해주는 과정 (가중치 벡터는 ZF, MMSE에 의해 얻어짐)
- Interference cancellation : 검출된 전송신호는 재생성되어, 수신 신호 벡터에서 빼주는 과정 또한 검출 방법에는 Non-linear기법과 linear기법이 있는데 낮은 BER과 높은 복잡도를 갖는 Non-linear 방법은 ML, 높은 BER과 낮은 복잡도를 갖는 linear기법인 ZF과 MMSE가 있다.
- ZF(Zero Forcing)
각 안테나로부터 얻는 2개의 수신 신호에 각 안테나에서 추정한 채널 특성 행렬의 역행렬 연산을 취함으로써 최초 송신신호를 구하는 방법이다.
ZF의 가중치 행렬은 𝑊zf=(𝐻(𝐻)𝐻)−1𝐻(𝐻) 와 같이 나타낼 수 있다.𝐻(𝐻)는 H의 Hermitian 전치 행렬이다.
송신 안테나의 개수가𝑁𝑇, 수신 안테나의 개수가 𝑁𝑅일 때, 송수신 신호의 관계는 y=Hx+z와 같이 나타낼 수 있다.
여기서 y=[y1,y2,...yNr]T이고, y1,y2,...,yNr은 j번째 수신 안테나에서 수신한 신호이고, x=[x1,x2,...,xNt]T이고, xi는 I번째 송신 안테나에서 송신된 신호이며, H의 (j,i)번째 element hji,j=1,2...,Nt는 I번째 송신 안테나와 j번째 수신 안테나 사이의 채널 이득을 나타낸다. z=[z1,z2,...,zNt]T이고, j번째 수신 안테나에서 받은 Gaussian 분포를 갖는 잡음성분이다.
- MMSE(Minimum Mean Square Error)
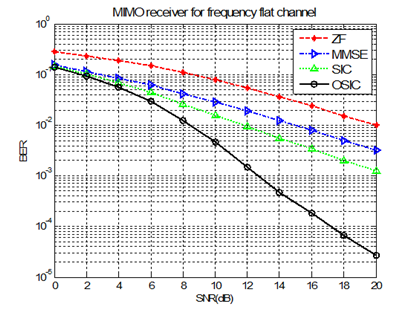
수신 신호에 대하여 채널 특성 행렬 상에서 발생하는 채널 간 간섭과 잡음 상승을 동시에 생각하여 가장 이상적인 에러를 갖는 연산을 취해주는 방식으로 일반적으로, ZF에 비해 MMSE가 우월한 성능을 보이는데, 이는 채널 이득행렬의 condition number가 클 경우 가중치를 곱할 때 발생하는 잡음증폭이 MMSE의 경우가 ZF에 비해 적기 때문이다. 따라서, SNR이 낮아 잡음의 크기가 클 때, MMSE와 ZF의 성능 차이가 크고, SNR이 높아 잡음의 크기가 작을 때는 두 가지 기법의 성능이 유사하게 된다. ZF 방식을 사용할 때 달성하게 되는 다이버시티 이득은 Nr-Nt+1이다. 송신 안테나가 하나인 경우에는 ZF 검출기법이 MRRC(Maximal Ratio Receiver Combing)기법과 동일하게 되고 달성하게 되는 다이버시티 이득은 Nr이다.
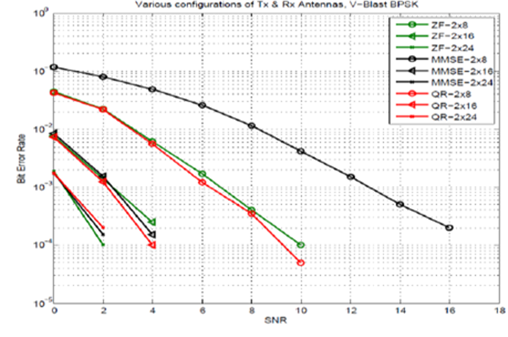
다. Turbo-BLAST
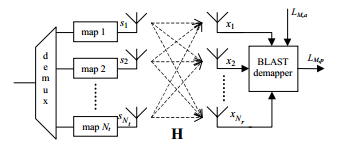
○ Channel coding 기법에 사용되었던 turbo code의 원리를 이용하여 만든 방법으로 각 layer마다 random space time interleaver를 경유하여 channel coding인 block coding과 modulation이 있다. 채널 코딩으로 error correction이 용이하며 변조 방법을 변경함으로써 높은 전송 성능을 가질 수 있다.
Encoder와 Decoder은 앞에 그림과 같이 나타나며 decoder는 반복이 가능하지만 구현상의 복잡도가 존재한다.
라. PARC(Per Antenna Rate Control)
○ PARC-N transmitter configuration
transmitter가 CQI(Chnannel Quality Indication)을 통해 수신자로 하여금 안테나당 가장 적합한 modulation과 coding scheme를 선택하게 하는 closed loop MIMO system에서 고려된 것으로 가장 일반적으로 PARC 4개의 전송 안테나를 가지는 것이다. 기존 V-BLAST의 경우 채널 상태 정보의 귀환 정보 없이 각 전송 안테나마다 동일한 변조와 부호화를 설정하여 전송하며 수신단에서의 귀환 정보를 이용하여 역다중화된 데이터 부스트림을 채널상태에 적합한 변조 및 부호화를 적용한 후 대역 확산을 거쳐서 각각의 전송 안테나를 통해 수신한다.
마. SVD
○ SVD는 real과 complex 행렬을 3개의 덩어리 행렬로 분해하는 것으로 Eigen decomposition처럼 행렬을 대각화하는 한 방법이다.
모든 mxn행렬에 대하여 적용이 가능하지만 EVD는 정방행렬에서만 가능한다. 또한, 임의의 mxn행렬에 대한 SVD는 아래식과 같다.
이때 , U = Unitary matrix , ∑: Diagonal matrix로 Matirxdml diagonal term을 singular value하고, V : Unitary matrix이다. singular value들이 MIMO 채널 용량을 결정하는데 중요한 역할을 한다.
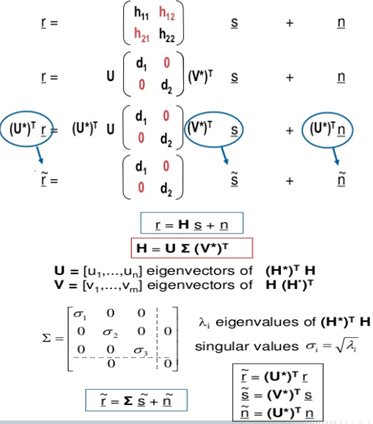
위에 그림은 다음 채널 행렬들을 만드는 방법에 대한 그림을 예시로 들고 있다.

행렬을 만드는 방법은 그 다음 그림에 나와 있듯이 MIMO channel 계산을 SISO 형태로 singular value decomposition을 통해서 계산 방법을 만드는 것인데 결론적으로 MIMO channel을 병렬 채널로 변환하여 통신 품질을 향상 시키도록 하지만 Throughtput이 감소하고 높은 복잡성을 갖게 된다. 따라서 계산량에 따라 알맞은 방법을 선택하는 것이 중요하다.
바. SIC
○ receiver가 동시에 도착하는 패킷을 디코드하기 위해서 허용되는 physical layer의 수용능력을 말하며 SIC는 receiver가 가장 강한 신호를 디코드하고 그 신호를 수신된 총 신호에서 제외한다. 다음으로 가장 강한 신호를 나머지 신호에서 추출하는 방법으로 이루어진다. 이는 다수의 패킷들로부터 정보를 복구하는 연속적인 과정으로 이루어지기 때문에 이름이 붙여졌다. SIC은 연속적으로 디코딩 된 스트림이면 각 단계에 이전에 디코딩 된 스트림의 영향은 제거되어 나타난다.
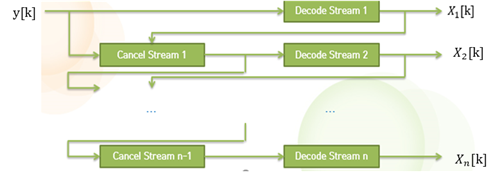
사. OSIC
○ OSIC는 V-BLAST 수신단에서 사용되는 기법으로 기본구조는 SIC와 동일하나 첫 번째 검출 데이터가 채널의 순서가 아닌 에러가 발생할 확률이 가장 낮은 채널부터 데이터를 검출함으로써 성능을 SIC보다 성능을 높이고자 하는 방법으로 검출 순서는 SINR을 기준으로 SINR이 높은 채널 순으로 정해진다. OSIC는 단지 검출 순서만을 바꿔줌으로써 SIC보다 우수한 성능을 보이게 되는 것이다.
OSIC 기법에서는 optimal ording detection과 Quasi-optimal ordering detection 방법이 존재하며 각각 검출 순서는 다음과 같다.
- optimal ordering detection
SNR이 가장 큰 신호부터 검출한다. 위 신호를 제거한 후 나머지 신호 중 가장 큰 SNR을 검출하는과정이다. 간섭을 제거시켜 성능을 향상시키고, 최적 검출 순서를 찾기 위해 매번 의사역행렬을 구해야 해서 복잡성이 증가한다.
- Quasi-optimal ordering detection
검출하기 위해 채널 행렬로부터 미리 SNR에 따라 검출순서를 결정하고 GSO 알고리즘을 통해 수신신호를 검출한다. 따라서 연산 복잡도가 감소하게 된다.
1. Ordering : Choosing the best channel (G)j is the jth row of G

2. Nulling : Nullifying the effect of the channel faced by kth stream

3. Slicing : Quantizing the nullified symbol with appropriate constellation

4. Canceling : Cancel the effect of detected stream from the received signal

5. Finding new channel matrix
6. Iteration
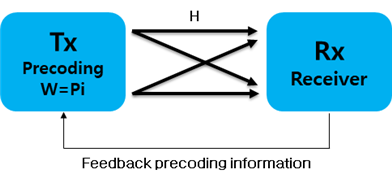
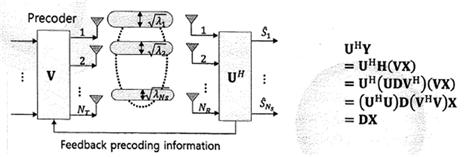
아. MIMO Precoding
○ 송신부 측에서 채널상태정보(CIS: Channel State Information)를 이용하여 데이터 전송의 신뢰성을 향상 시키는 기법이다. 채널 상에서 발생되는 페이딩 및 간섭에 대한 정보에 근거하여 생성된 프리코딩 행렬을 이용하여 전송될 데이터를 코딩한 후 전송한다.
 |
 |
 |
|
자. Beamforming
○ 안테나의 빔이 해당 단말에게만 국한하여 비추도록 하는 기술이다.

- 2D Beamforming
only Horizontal(Azimuth) angel
- 3D Beamforming
Horizontal(Azimuth) + Vetical(Zentih, Elevation) angle

'컴퓨터 과학 및 기술 연구 > 통신공학이론' 카테고리의 다른 글
| "이동통신시스템의 핵심 기술" 이론 정리 6편( OFDM & OFDMA & SC-FDMA) (3) | 2024.01.30 |
|---|---|
| "이동통신시스템의 핵심 기술" 이론 정리 4편(Source coding & Channel coding & Interleaver) (0) | 2024.01.29 |
| "이동통신시스템의 핵심 기술" 이론 정리 3편(Modulation / Demodulation) (2) | 2024.01.27 |
| "이동통신시스템의 핵심 기술" 이론 정리 1편(Multiple Access) (1) | 2024.01.26 |
| "광통신시스템의 핵심을 알면 세상이 바뀐다" 기초 이론 정리편 (1) | 2024.01.25 |


댓글