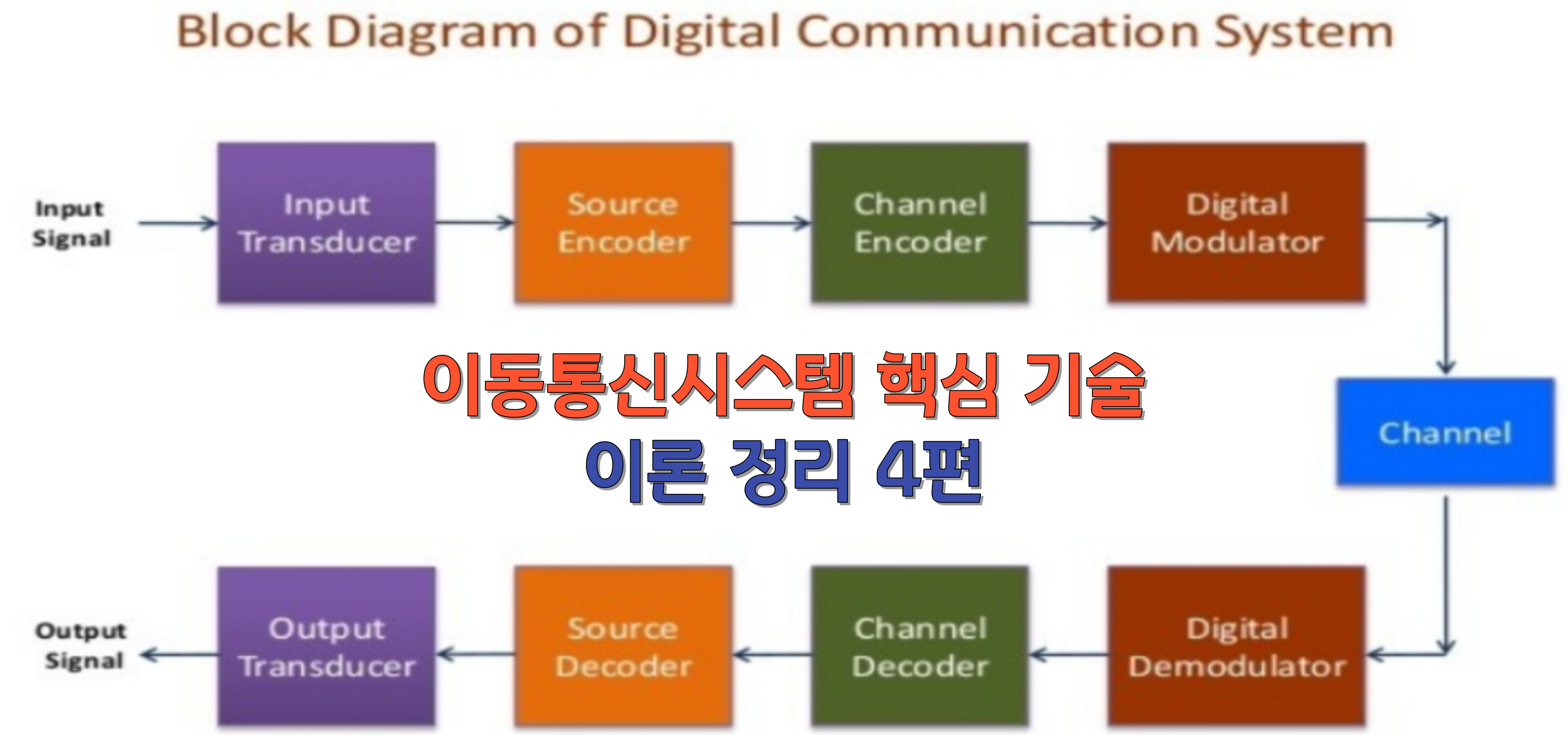
1. Source coding concept
○ 정보신호에서 디지털 부호를 만드는 과정을 encoding, 부호를 해독하여 본래의 신호를 만드는 과정을 Decoding이라고 한다. 이 두 가지 과정을 처리하는 방법을 합쳐서 부호화 방식이라고 한다. 부호화 방식은 사용 목적에 따라 크게 원처부호화방식과 채널부호화 방식으로 나뉜다.
○ Source coding
원천부호화(source coding)는 정보신호를 전송하기에 적합하도록 효율적으로 부호화하는 데 목적이 있다. 원래의 정보 신호를 디지털 신호로 바꾸고 데이터를 변환, 압축하여 제한된 대역폭에서 고속으로 전송되도록 한다. 소스의 효율성을 높이기 위해 평균코드길이의 최소화를 지향한다. 원천부호화는 에러가 발생했을 때 오류검출 및 정정 능력이 매우 취약하다. 특히 고속의 데이터 망(network)에서는 신뢰성 있는 데이터 전송 시스템이 필요하다.
다른 말로는 섀넌의 제1부호화 정리라고도 한다. 잡음이 없는 통신로에 관한 것으로 정보원의 엔트로피가 H 섀넌/문자, 통신로 용량이 C 섀넌/초일 때, 이 통신로를 통하여 C/H문자/초에 가까운 속도로 정보를 보내는 부호화가 존재함을 나타낸 것이다. 정보원에서 발생하는 통보를 부호화할 때 이 부호의 평균 길이의 한계를 주는 형태로 나타낼 수도 있다.
가. Shannon 정리
○ 섀넌의 제1부호화정리
정보 엔트로피(영어: information entropy)는 클로드 섀넌(영어: Claude E. Shannon)이 제안한 개념으로 신호나 사건에 있는 정보의 양을 엔트로피의 개념을 빌려 설명한 것이다. 정보 이론에서 엔트로피는 어떤 확률변수의 불확실성(영어: uncertainity)을 측정하는 것이다. 섀넌 엔트로피라고도 불리는 엔트로피는, 어떤 메시지가 포함하고 있는 정보 양의 기대 값을 나타내며 주로 비트(bit) 단위로 표시한다.
통신로 용량이 C(비트/초)인 이상적인 통신로에서, 어떤 정보원을 R(비트/초)의 속도로 부호화하고, 이 통로를 통해 전송한다. 만약 R가 C보다 작다면 이 정보원의 정보를 얼마든지 작은 애매도(오류확률)로 전송하는 부호화 방법이 존재한다.
○ 정의
이산랜덤변수 X가 각각 확률 값 {x1, ..., xn}을 가질 때 엔트로피 H는 다음과 같이 표현될 수 있다.
H(X) = E((I)X))
여기서 E는 기대 값을 나타내고 I는 X의 정보량을 의미한다.
I(X) 또한 랜덤변수인데, 만약 p가 X의 확률질량함수를 나타낸다면 엔트로피는 다음과 같이 표현할 수 있다.

사건 x의 엔트로피는 x의 모든 가능한 결과값 i에 대해 i의 발생 확률 값인 과 그 확률의 역수의 로그 값의 곱의 합이 된다. 이 정의는 이산 사건 대신에 적분을 사용하여 임의의 연속 확률 분포에 대해 확장할 수 있다.
위의 식에서 지수 b는 로그에서 사용되는 지수를 의미한다. 일반적으로 지수 b의 값으로서 2, e, 또는 10이 많이 사용된다. b=2인 경우에는 엔트로피의 단위가 비트로 사용되고 ,b=e일땐 네트(nat), 그리고 b=10인 경우에는 디짓(digit)이 사용된다.
어떤 i에 대하여 pi =0 인 경우에는 앞서 정의된 수식에 따라서 0 logb 0 이 되므로 다음과 같은 한계 값을 정의할 수 있다.
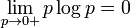
○ 엔트로피
일반적으로 불확실성(Uncertainty)에 대한 양(값)을 말하며, 통신 분야(정보공학)에서는 정보원(Information Source)의 평균 정보량을 말한다. 여기서 말하는 정보는 "정보의 의미/내용" 보다는 "정보의 양"을 중시하며 따라서, 평균정보량/최대정보량/효율성과 같이 정보량의 측정이 중요한 관점이다.
엔트로피(평균 정보량)를 선택 가능한 심볼 집합에서 `심볼 당 평균 정보량(비트수)`로 표현할 수 있으며 수식으로 나타내자면, 아래와 같은 식으로 나타낼 수 있다.
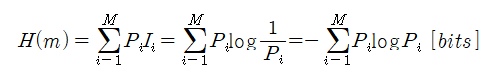
- (m : 메세지 심볼 집합, 심볼의 개수 : M개, P : 발생 확률, I : 정보량)
엔트로피가 낮다는 의미는, 확정적인 정보가 많으며, 특정 심볼이 발생할 확률이 높다는 것을 의미한다. 또한 불확실성이 낮다는 의미이기 때문에 이와 반대의 개념인 예측성이 높다진다는 것을 이야기 한다.
엔트로피가 높다는 이야기는 전혀 예측이 불가능하며 놀라운 정보가 많을 가능성이 있다는 것을 의미한다. 또한 각 심볼들의 발생 확률이 동일함하기 때문에 무작위성이 높고, 랜덤성이 높다. 또한 중복성이 거의 없다. 이 뿐 아니라 평균 정보량이 높다. 하지만 통신채널 관점에서 쓸모없는 채널일 경우가 많은데, 그 이유는 너무 완벽한 랜덤성 혹은 무예측성을 갖게 되기 때문이다.
0 ≤ H(m) ≤ log2 M
위의 식에서 엔트로피 하한값 즉 최소 조건인 경우는 H(m) = 0인 경우이다. H(m) = 0의 의미는 각 심볼 중 오직 하나가 발생확률이 1 이고, 나머지 심볼들의 발생확률이 0 일 때를 의미하며 확실성이 있음을 의미한다. 이와 반대로 엔트로피 상한값 즉 최대 조건은 H(m) = log2 M인 경우이고 소스 알파벳 내의 모든 심볼들이 동일한 발생확률을 갖을 때 (Pi=1/M) 이때의 엔트로피가 log2 M임을 의미한다. 이때의 불확실성은 가장 높다.
소스 데이터에 있는 모든 정보를 표현하기 위한 필요 최소 비트 수는, 소스의 평균적 불확실성인 엔트로피 값에 의해 결정된다. 따라서, 소스의 정보 효율성(Efficiency) = (엔트로피 [bits]) / (소스 표현 비트수 [bits]) x 100 %
로 나타낼 수 있으며 어떤 부호화도 소스(정보원)가 갖는 엔트로피 보다 적은 정보량으로 압축할 수 없다. 이는 데이터로부터 불필요한 정보를 제거(압축)하는 데의 한계치를 제공한다. 고로 일반적으로, 얻을 수 있는 평균정보량(엔트로피)이 가능한 최대가 될 수 있도록 통신시스템을 설계하여야 한다. 만일 정보원의 엔트로피(평균정보량)가 채널용량 보다 작으면, 그 채널을 통해 에러가 없는 통신이 가능한다. 만약 각 소스가 통계적 독립이면
=> H(A,B) = H(A) + H(B) => 즉, 전체 정보량은 각 소스의 정보량들의 총합과 같을 의미하고 각 소스가 종속적이면
=> H(A,B) = H(A) + H(B|A) 결국, H(A,B) ≤ H(A) + H(B) 이다.
(등식은 A,B가 서로 통계적으로 독립일 때)
2. Huffman, Run length, Gray
가. Huffman code
○ 전산학과 정보 이론에서 허프만 부호화(Huffman coding)는 무손실 압축에 쓰이는 엔트로피 부호화의 일종으로, 데이터 문자의 등장 빈도에 따라서 다른 길이의 부호를 사용하는 알고리즘이다. 1952년 당시 박사과정 학생이던 데이비드 허프만이 A Method for the Construction of Minimum-Redundancy Codes[1]란 제목의 논문으로 처음 발표했다.
허프만 부호화는 문자들의 빈도로부터 접두 부호(어떤 한 문자에 대한 부호가 다른 부호들의 접두어가 되지 않는 부호)를 만들어 내는 알고리즘으로, 적게 나오는 문자일수록 더 긴 부호를 쓰고 많이 나올수록 더 짧은 부호를 쓴다. 허프만 부호화는 주어진 빈도에 대해서 항상 최적의 접두 부호를 만들어 내며, 이 과정은 빈도가 정렬되어 있을 경우 O(n)만에 가능하다. 각 문자들의 빈도가 2의 거듭제곱 꼴이거나 모두 같을 경우 이 접두 부호는 간단한 이진 블록 부호와 동일하다.
허프만 부호화가 항상 최적의 접두 부호를 만들어 내기는 하지만, 접두 부호가 아닌 다른 종류의 부호가 더 효율적일 수도 있다. 예를 들어 여러 문자를 하나의 부호로 묶어 표현할 수 있는 산술 부호화나 LZW 등이 허프만 부호보다 효율적인 경우가 많으며, 이것은 대부분 하나의 기호를 정수개의 길이를 가진 부호로서 표현하도록 되어 있는 한계에서 기인한다.
위에서 아래로 진행하는 샤논파노방법과는 달리 허프만 알고리즘의 부호화 순서는 아래에서 위로 진행한다.
○ 알고리즘
①초기화 : 모든 기호를 출현 빈도수에 따라 나열한다.
②단 한 가지 기호가 남을 때까지 아래 단계를 반복한다.
㉠목록으로부터 가장 빈도가 낮은 것을 2개 고른다.
㉡그 다음 허프만이 두가지 기호를 부모 노드를 가지는 부트리를 구성하고 자식노드를 생성한다. 부모 노드 단 기호들의 빈도수를 더하여 주 노드에 할당하고 목록의 순서에 맞도록 목록에 삽입한다.
㉢목록에서 부모노드에 포함된 기호를 제거한다.
*허프만 알고리즘은 입력 기호를 잎으로 하는 이진 트리를 만들어서 접두 부호를 만들어 내는 알고리즘이다.
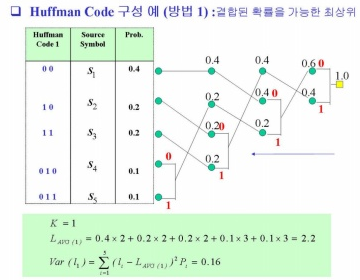
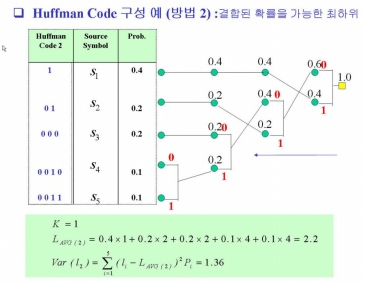
○ Reduction process
①발생 확률이 가장 낮은 두 개의 심볼을 결합하여 그 합의 확률을 갖는 하나의 심볼을 만들어 소스 심볼의 개수를 한 개씩 축소한다.
➁새로이 발생된 심볼이 확률을 나머지 확률들과 비교하여 해당되는 위칠 천이시킨다.
③위 1,2 과정을 두 개의 심볼만 남을 때 까지 반복한다.
○ Splitting (Epansion) Process
①축소 과정으로 남아 있는 두 개의 심볼에 각각 "0"과 "1"을 할당한다(splitting)
②두 개의 심볼 중 축소과정의전 단계에서 결합되었던 하나의 심볼에 대하여 다시 두 개로 확장하면서 각각 "0"과 "1"을 덧붙인다(Expansion)
③위 2 과정을 소스 심볼의 개수까지 반복한다.
 |
 |
○ 허프만 코드와 아스키 코드 비교
예를 들어, 특정 문서가 영문자 a, b, c, d, e, f, g, h로만 이루어져 있다. 그리고 각 문자의 문서에서 나타나는 확률이 아래의 표와 같다고 합시다.
| 문자 | 확률 값 |
| a | 0.3 |
| b | 0.2 |
| c | 0.15 |
| d | 0.1 |
| e | 0.1 |
| f | 0.05 |
| g | 0.05 |
| H | 0.05 |
이 문서를 위해 압축을 고려하지 않은 일반적인 코드를 생성한다고 하면, 총 8개의 글자이므로, 23 = 8, 에서 총 3비트가 필요할 것입니다. 각 글자에 아스키 코드와 같은 방식, 즉 압축을 고려하지 않는 방식으로 코드를 부여한다면
| 문자 | 코드 |
| a | 000 |
| b | 001 |
| c | 010 |
| d | 011 |
| e | 100 |
| f | 101 |
| g | 110 |
| h | 111 |
이렇게 코드를 부여하는 방식이 바로 ASCII 코드에서 사용인데 이 문서에서 각 문자가 나타날 확률이 다르기 때문에, 더 많이 나타나는 문자에 더 짧은 코드를 부여한다면 문서의 크기를 줄일 수 있을 것이다. 각 문자들이 나타나는 확률을 반영해 각 문자에 코드를 부여한다면, 아마 다음과 같은 코드를 생성할 수 있다.
| 문자 | 코드 |
| a | 11 |
| b | 00 |
| c | 101 |
| d | 010 |
| e | 1000 |
| f | 1001 |
| g | 0110 |
| h | 0111 |
문서의 대부분을 차지하는 a, b에 2비트의 코드를 부여함으로써, 문서의 크기를 상당량 줄일 수 있다. 기존 방식에서는 코든 글자들에 똑같이 3비트가 부여되어 있으므로, 3비트씩 끊어서 읽어 문자들을 해독할 수 있지만, 위와 같이 각 글자마다 코드 길이가 다르게 되어 있을 때는 문서의 디코딩이 제대로 이루어 질 것인가에 대해 의문을 가질 수 있다.
다음의 예를 살펴보도록 하자. 예를 들어, bcgaaaefh 라는 문자열을 바로 위의 코드 체계로 인코딩 해보면, 다음과 같은 코드가 된다.
* 인코딩 결과 *
001011111111000100101110110
* 디코딩 과정 *
그럼 위의 인코딩된 코드를 디코딩해서 bcaaaefhg 문자열을 얻는 과정을 살펴보자.
가장 짧은 코드 길이가 2비트임으로, 처음 2비트 읽어오면 00이다. 이는 위 코드표의 b와 일치한다. b를 출력한후 다음 2비트를 읽으면 10이다. 이 코드와 일치하는 문자가 없으므로, 한 비트를 더 읽어 오면 101이 되고 이는 c와 일치하므로 c를 출력한다. 이와 같은 방식으로 인코딩된 코드에서 한 비트씩 읽어온 후, 코드표에 일치하는 문자가 있는지 검사하여 일치한 문자를 출력함으로써, 디코딩이 제대로 이루어지게 된다. 위의 코드 표를 자세히 살펴보면, 한 문자의 코드는 다른 코드의 처음 부분과 일치하지 않는 특징을 발견할 수 있다. 예를 들어, a의 코드는 11인데 이를 다른 코드들의 처음 2비트와 비교해 본다면 11로 시작되는 코드가 하나도 없음을 알 수 있다. 마찬가지로 d의 코드는 010인데 010으로 시작하는 코드는 d외에 하나도 없는 것을 확인할 수 있다. 바로 이런 종류의 코드를 prefix code(더 정확히 prefix-free code)라고 한다. 그렇다면, 어떻게 이런 prefix code를 생성할 수 있을까? 문자들의 개수가 위와 같이 8개 정도로 작을 때면, 간단히 손으로 써보면서 각 문자들의 코드를 정할 수 있겠지만, 기호의 개수가 많을 때는 이런 방법은 불가능 할 것이다. 따라서, 각 기호에 적절한 코드를 부여하는 알고리즘이 필요한데, 그것이 바로 허프만 코딩 알고리즘이다.
○ 허프만 트리

허프만 코드를 생성하기 위해 사용되는 허프만 트리이다. 트리의 리프 노드는 문자와 그 확률을 저장하고 있고, 중간 노드는 자식 노드의 확률을 합한 값을 저장하고 있다.
가지의 왼쪽 부분에는 숫자 0, 1이 있는 것을 볼 수 있는데, 이는 각 문자들의 코드를 이루고 있는 비트로써, 루트 노드에서 각 리프 노드의 이르는 가지들의 숫자들이 그 문자의 코드가 되고, 이는 표 1 에 나타나는 각 문자의 코드와 일치한다. 문자들의 허프만 코드를 생성하는 것은 바로 위 허프만 트리를 구축하는 것인데, 허프만 트리를 구축 알고리즘은 다음과 같다.
○ 허프만 트리 생성
허프만 트리를 생성하기 위해서는 트리의 노드를 저장하는 두 개의 큐(큐1, 큐2)가 필요.
①인코딩 하려는 모든 문자과 그 확률 값을 갖는 리프 노드를 생성한다.
②모든 리프 노드를 큐1에 넣는다.
③큐1과 큐2에, 두 개 이상의 노드가 있을 때까지 다음을 반복한다.
㉠큐1과 큐2에서, 어느 큐에서든 상관없이, 확률이 가장 낮은 두 개의 노드를 꺼낸다. ㉡방금 꺼낸 두 개의 노드를 자식 노드로 갖는 중간 노드를 생성하고 생성한
중간노드의 확률 값은 두 자식 노드의 확률 값을 더한 것으로 한다.
㉢생성한 중간 노드를 두 번째 큐에 넣는다.
④마지막에 남은 하나의 노드가 루트 노드이다. 허프만 트리가 완성된다.
| 문자 | 확률 값 |
| a | 0.3 |
| b | 0.2 |
| c | 0.15 |
| d | 0.1 |
| e | 0.1 |
| f | 0.05 |
| g | 0.05 |
| H | 0.05 |
○ 허프만 트리 알고리즘 적용
다음 표에 나타나는 문자들을 위 알고리즘에 적용하는 과정을 살펴보면
먼저, 각 문자와 그 확률 값을 갖는 노드를 생성하여 큐1에 넣는다.
| 큐1 | a(0.3), b(0.2), c(0.15), d(0.1), e(0.1), f(0.05), g(0.05), h(0.05) |
| 큐2 |
| 큐1 | a(0.3), b(0.2), c(0.15), d(0.1), e(0.1), h(0.05) |
| 큐2 | ①(0.1) |
큐1과 큐2에서 가장 작은 확률 값을 갖는 노드 중, e와 h를 꺼내, 이 노드를 자식 노드로 갖는 중간 노드를 생성한다.
| 큐1 | a(0.3), b(0.2), c(0.15), d(0.1) |
| 큐2 | ①(0.1), ②(0.15) |
다음으로 작은 확률 값을 갖는 노드 2개를 선택하면, ①과 d가 선택되고, 다시 위 과정을 반복한다.
| 큐1 | a(0.3), b(0.2), c(0.15) |
| 큐2 | ②(0.15), ③(0.2) |
○ 허프만 트리 알고리즘 특징
- 무손실압축
- 사용 : JPEG
- 압축률 : 매우 좋음

나. Run-length coding
○ 런 렝스 부호화(Run-length encoding, RLE) 또는 런 길이 부호화는 매우 간단한 비손실 압축 방법으로, 데이터에서 같은 값이 연속해서 나타나는 것을 그 개수와 반복되는 값만으로 표현하는 방법이다. 이 방법은 아이콘 등의 간단한 이미지와 같이 연속된 값이 많이 있는 데이터에 효과적이다. 런 렝스 부호화는 만화나 애니메이션 등과 같이 배경의 변화가 없는 영상에 적합한 방식이다. 그러나 실제적으로 잘 적용되지 못한다. 이 방식은 3번 이상 반복되는 문자들에 대해 이용되기 때문에 영어 문장에서는 잘 수행되기 어렵다.
○ 예제
흰 바탕에 검은 글자가 나오는 스크린을 생각하면 이 스크린에는 연속된 흰 픽셀이 많이 나타날 것이다. 이러한 스크린의 한 스캔 라인이 다음과 같다고 가정하자. (흰 픽셀을 W로 표시하고 검은 픽셀을 B로 표시한다.)
WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWW
위의 데이터를 간단한 반복 길이 부호를 사용해서 압축하면 다음결과를 얻을 수 있다.
12WB12W3B24WB14W
이는 '12개의 W, (한 개의) B, 12개의 W, 3개의 B, 24개의 W, (한 개의) B, 14개의 W'로 해석한다. 위의 예제의 경우, 압축 전에는 67글자였으나 압축 후에는 단지 16글자만으로 표현할 수 있다. 물론 실제로 이러한 이미지는 바이너리 포맷으로 저장되며 반복되는 길이를 저장하는 방법도 다양하지만, 기본적인 개념은 동일하다. 이때 데이터의 크기는 67바이트에서 16바이트로 줄었으므로 압축률은 약 4.18이다.
○ 활용
반복 길이 부호화를 사용하는 대표적인 파일 형식으로 PCX, BMP, ILBM 등이 있다.
반복 길이 부호화는 BWWBWWBWWBWW와 같이 데이터가 일정한 패턴을 따르는 경우를 처리할 수 없으며, 이런 경우 LZ77이나 LZ78 계열 알고리즘들이 유리하다. 또한 이 방법은 연속된 색조로 이루어진 이미지에도 그리 잘 사용되지 않으며, 이런 용도로는 별도의 변환과 양자화를 사용하는 JPEG와 같은 방법이 사용된다.
○ 가역 부호와와 비가역 부호화
①가역 부호화 : 복호시 원래의 데이터와 일치하는 부호화
➁비가역 부호화 : 복호시 원래의 데이터와 일치하지 않는 부호화
라고 할 수 있다. 가역 부호화는, 주로 데이터의 통계적인 성질을 이용하여 압축한다. 즉, 어떤 값이 상당히 크다든지, 연속하여 같은 값이 자주 나온다든지 하는 성질이다. 이 성질을 이용하여 뒤이어 논할 run length 부호화와 DPCM, 가역길이 대부호화를 이용하여 부호화하면 데이터를 잃지 않고 압축할 수 있어 복호화해서도 원래의 데이터로 돌아갈 수가 있다. 그러나 데이터의 통계적인 성질을 이용하기 때문에, 데이터를 밀도 있게 압축하는 경우와 그렇지 못하는 경우가 있다. 이러한 가역 부호화에 비하여, 비가역 부호화는 데이터의 정보를 일부 삭제하고 압축하기 때문에 복호화한 데이터는 원래의 데이터와 일치하지 않는다.
예를 들면, 아래 그림에서 볼 수 있는 것과 같이 화소 데이터를 일정 간격 등으로 솎아냄으로서 전체의 데이터 수를 줄이는 방법과, 그림 (b)와 같이 1화소값당 비트수를 줄이는 방법을 생각할 수 있다.
X O X O X O X O X O O O O O O O O O O @
O X O X O X O X O X O O O O O O O O O O
X O X O X O X O X O O O O O O O O O O O
O X O X O X O X O X O O O O O O O O O O
(a) (b)
X : 버린 화소 데이터 O : 남아있는 화소 데이터
그러나, 이와 같이 단순하게 화소의 수를 줄인다든지, 데이터의 비트수를 줄인 다든지 하면, 복호할 때에 그림이 흐려진다든지, 물체의 형태가 왜곡된다든지, 의사윤곽이라 불리는 어색한 윤곽선이 출력된다든지 하며 영상의 질이 떨어지게 된다. 영상의 질이 떨어져도 좋다면, 얼마든지 데이터를 감소시키는 것이 가능하지만, 영상의 질을 될 수 있는 한 좋게 하고, 데이터량을 줄이기 위해서는 여러 가지 기법이 필요하게 된다. 실제로 대부분의 영상 데이터 압축에서는 인간의 눈에 잘 띄지 않는 고주파 성분을 감소시킨다든지 하여 많은 비중을 차지하지 않는 정보만을 삭제하고 있다.
(참조:http://terms.naver.com/entry.nhn?docId=2270341&cid=51173&categoryId=51173)
○ 2진영상의 부호화(run length 부호화
부호화의 기본 과정인 "0"과 "1"로서 데이터를 표현하는 2진 영상의 데이터 압축에 대해서 알아보자. 2진 영상의 데이터 부호화 기법으로서 대표적인 부호화 방법으로는 run length 부호화가 있다. 이부호화는 연속하는 "0" 또는 "1"의 개수를 하나의 부호로서 나타내는 방법이다. 결국, 연속하여 같은 값을 가지는 데이터가 있다면, 그 길이(run length)를 이용하여 부호화하는 방법이다. 이 부호화 방법의 한 예를 아래에 나타내었다.
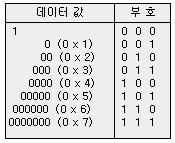
이 부호를 사용하여 다음의 데이터를 부호화해 보자.
0000100000001000000100000001
위의 데이터는 29개의 "0"과 "1"로 이루어져 있다. 따라서, 이 데이터를 원래의 비트로 표현하면, 29비트가 된다. run length 부호화에는 다음에 나타낸 것과 같이 연속하는 "0"의 데이터를 모아서 8개로 부호화한다.

○ 각각의 값은 표의 run length 부호를 사용하면, 각각 3비트씩, 합계 24 비트가 되고, 원래의 비트로 표현하는 것보다도 적은 비트 수로서 표현할 수 있게 된다. 이와 같이 run length 부호를 사용하면, 여러 데이터를 압축할 수 있으므로 팩스 등에 이용되고 있다.

○ Gray code
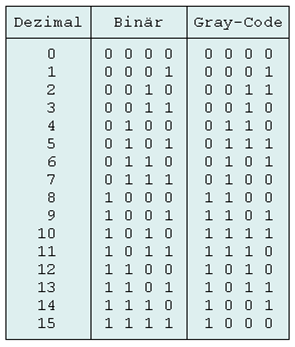
그레이 코드란 ‘0’과 ‘1’의 조합으로 모든 상태를 나타내는 코드로써 인접한 상태로 변화 할 때 단지 하나의 비트만이 변화되는 최소 변환 코드의 일종이다. 그레이 코드는 각 자리에 일정한 가중치가 부여되지 않는 비가중치 코드 이므로 연산에는 적합하지 않지만 다음 코드와 한 비트만 다르다는 특징 때문에 입출력 장치, A/D 변환기 등에 많이 사용된다.

이전 표는 그레이 코드와 2진 코드를 비교하여 나타내었다. 그레이 코드의 경우 다음 코드와 오직 한 비트만이 다름을 확인할 수 있다. 2진 코드의 경우 각 비트가 LSB로부터 1, 2, 4 값의 가중치를 갖는 반면 그레이 코드는 각 자리에 가중치가 부여되지 않는다.
○ n bit 그레이 코드 생성
n bit 그레이 코드는 n-1 bit 그레이 코드를 이용하여 생성할 수 있다. 먼저 n-1 bit 그레이 코드 리스트를 역순으로 정렬하여 원래의 n-1 bit 그레이 코드 리스트 뒤에 이어 붙이고MSB+1 자리에 한 비트를 추가하는데 기존 리스트의 원소에는 ‘0’을 반전된 부분의 원소에는 ‘1’을 각각 추가한다. 그림[2-다-1]은 3비트 그레이 코드 생성 과정을 나타내었다.
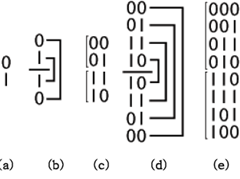
그림 1의 (b)와 같이 1 bit 그레이 코드를 반전시켜 덧붙이고 ‘0’, ‘1’을 각각의 리스트원소의 상위 비트에 추가시켜 그림 1의 (c)와 같이 2 bit 그레이 코드를 생성한다. 3 bit의 경우에도 같은 과정을 거쳐 완성하면 그림 1의 (e)와 같은 모습이 된다.
○ 그레이 코드와 2진 코드의 상호 변환
2진 코드 ↔ 그레이 코드 변환은 간단한 비트 연산을 통해 이루어진다. 먼저 2진코드를 그레이 코드로 변환하는 방법을 살펴보면, 2진 코드의 MSB는 그대로 그레이 코드의 MSB가 되고 2진 코드의 MSB부터 이웃한 두 비트를 XOR 한 결과를 차례로 그레이 코드의 다음 비트로 정한다. 그레이 코드를 2진 코드로 변환하는 방법은 MSB는 그대로 그레이 코드의 MSB가 되며 얻어진 그레이 코드의 첫번째 비트(MSB)와 2진코드의 두번째 비트를 XOR 하여 그레이 코드의 두번째 비트를 생성한다. 마찬가지 방법으로 그레이 코드의 n번째 비트와 2진 코드의 n-1번째 비트를 XOR 하여 그레이 코드의 n-1번째 비트를 생성하고, 이 과정을 반복하여 그레이 코드를 완성한다. 그림[2-다-2]에서는 그레이 코드와 2진 코드의 변환 방법을 나타내었다.

○ 그레이 코드의 규칙성
2진 코드의 경우 현 상태에서 1을 증가시켜 다음 상태를 쉽게 구해낼 수 있지만 그레이 코드의 경우 규칙성을 찾기란 그리 간단하지 않다. 가장 먼저 생각할 수 있는 방법은 앞에서 언급한 그레이 코드와 2진 코드의 변환을 이용한 방법인데 현 상태의 그레이 코드를 2진 코드로 변환하여 1을 증가시킨 후 다시 그레이 코드로 변환하는 방법이다. 이 방법은 구현하기는 어렵지 않지만 2진 코드의 증가 연산을 거쳐야 하기 때문에 한 스텝에 한 비트만 달라지는 그레이 코드의 이점을 살릴 수가 없다. 변환 과정을 거치지 않고 그레이 코드의 규칙성을 이용하여 다음 상태를 구하는 하나의 방법을 알아본다.
4 bit 그레이 코드를 G[3:0] 이라 할 때 G[0] (LSB) 는 상태가 변할 때 마다 0과 1이 두번씩 나타나는 주기성을 가지고 있다. 표 2의 (a)에서와 같이 매번 0과 1이 반전되는 비트 C를 삽입하면 C가 0일 때 다음 상태에서 G[0]이 변환되는 것을 볼 수 있다. 표 2의 (b), (c), (d)를 보면 G[1], G[2], G[3]은 한자리 아래 비트가 1, C가 1, 그리고 그 사이의 비트가 0이 될 때 즉 각각 ‘11’, ‘101’, ‘1001’와 같은 패턴을 보일 때 다음 상태에서 비트 값이 반전되는 것을 볼 수 있다. 한 가지 예외는 G[3]의 경우 마지막 ‘1000’에서 ‘0000’으로 다시 돌아갈 때 한자리 아래 비트가 1이 아니어도 다음 상태에서 바뀌는 것을 볼 수 있다. 이 같은 규칙을 도식화 하면 표[2-다-2]와 같다. n bit의 그레이 코드 G[n-1:0]를 입력으로 받아 다음 상태의 그레이 코드 G’[n-1:0]을 출력한다.
3. Channel coding concept
○ 디지털 전송신호에 어떤 부수적인 잉여 비트를 삽입하여 전송 시 채널에 가해지는 각종 잡음으로 인한 에러를 검출·정정하는 기능을 채널코딩 이라고 한다. 채널 부호화에는 블록 부호화 방식(block coding method)과 돌림형 부호화 방식(convolutional coding)이 있다. 블록 부호화는 블록 단위로 부호화 및 복호화를 행하고, 돌림형 부호화는 블록 단위로 하지 않고 일정 길이의 메모리를 이용해 이전 데이터와 현재 데이터를 비교해 부호화를 수행한다.
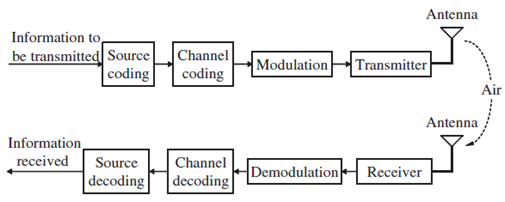
채널 부호화는 성능의 열화 없이 전송 조건에 대응하여 신호의 전력과 신호의 대역폭을 상호 교환한다. 그러나 셀룰러 시스템에서는 최종단의 통신 선로가 기지국과 단말국 사이의 채널이고, 단말기의 위치에 관계없이 접속 가능하고 단말기의 이동성을 보장하기 위하여 신호는 반드시 잡음이 많은 자유 공간을 통과해야만 한다. 채널 부호화는 이산 디지털 정보를 신뢰성과 보안성에 초점을 두어 채널을 통한 전송에 보다 적합하도록 만드는 과정이다. 즉, 채널 부호화는 비트 오류율 또는 프레임 오류율로 표현되는 전송 품질의 적합성을 보장하는 기술이다. 채널 부화화의 배경이 되는 기본 원리는 데이터열에 잉여분을 더함으로써 수신기가 전송 오류를 찾아내거나 고치게까지 하는 것이다.
① 채널 부호화 (Channel Coding)
- 채널을 통한 정보의 전송 중에 수신측이 오류를 검출, 정정할 수 있도록 송신원에서의 신호 변환 과정
- 에러검출 및 에러정정
채널 상의 에러(잡음,간섭,페이딩 등)를 극복하기 위한 사전 성능 향상 과정
- 순방향 오류제어(FEC)의 일종
- 각 데이터 심볼을 나타내는 코드 시퀸스 간에 두드러진 차이를 나게하여 다른 코드 시퀸스로 오인될 가능성을 줄이도록 데이터 시퀸스를 확장 변환시키는 것
② 채널 부호화에 관련된 주요 개념을 설명하는 용어
- 채널의 용량한계 => 채널 용량
전송의 고속성을 이룰 수 있는 한계용량을 채널용량이라고 한다.
채널용량은 "오류가 없는 상태"로 유지할 수 있는 전송속도 상한을 말한다.
- 채널에 대한 근사 모델 => 채널 모델
에러제어 등을 위한 여유정보분 => Redundancy
- 채널부호화 과정은 일반적으로 원래의 코드 길이가 길어지며(잉여비트 추가),
이 길어진 부분을 Redundancy라고 한다. 사실 이 Redundancy에 의해 "오류의 제어"가 가능하여 전송의 신뢰성과 고속성을 달성할 수 있게 된다.
부호화를 위해 어느 정도의 비트를 사용하는가 => 부호율
부호화에 따른 이득의 량(量)은 (성능 개선) => 부호화 이득
○ 일반적인 AWGN 환경하에서 요구되는 BER(Bit Error Rate)에 도달하기 위한 Eb/No의 감소량
③ 채널부호화 분류
- 오류의 검출 및 정정 여부에 따른 구분
- 오류검출코드
. 단지 전송 중에 발생한 오류 만을 검출할 수 있게함
. 한편, 재전송(Retransmission)이 가능한 시스템에서는 오류정정 체계를 갖추지 못하였더라도, 단지 오류의 검출만으로도 오류제어가 충분한 경우가 많다.
- 오류정정코드
. 오류의 검출 및 수정이 모두 가능
- 오류의 영향을 덜 받도록하는 기술에 따른 분류
- 구조화 코딩 (Structured Coding)
. 오류의 탐지 및 정정에 필요한 여분의 비트(패리티 비트 등)들을 데이터 를 비트열에 첨가시킴
. 종류) 블록 코딩, 비블록 코딩
- 기억(memory) 여하에 따른 구분
블록 코드(Block Code) 형태 => 블록 부호화 (Block Coding)
. 부호화기가 메모리(기억성) 없음
. 종류) Linear Code (선형 부호), Cyclic Code (순회 부호)
. 예) Hamming Code, Reed-Solomon Code 방식 등
- 비블록 코드(Non-Block Code) 형태 => 콘볼루션 부호화 (Convolutional Coding)
. 부호화기가 메모리(기억성) 있음
. 블록 코드 방식과의 근본적인 차이로써 부호화기가 메모리를 갖고 있음
. 즉, 코드화시킬 때 현재 입력되는 신호 및 과거의 일부 신호를 함께 활용
. Viterbi Code, Turbo Code 방식 등
④ 채널부호화 특징
- 채널부호화의 목적
전송 데이터에 구조화된 잉여정보(Redundancy)를 삽입함으로써 제한된 전력 또는 제한된 대역폭을 갖는 채널 환경에서 비트오류율(BER) 성능을 개선시키기 위함
- 부작용(단점)
. 여분의 비트들로 인해 채널 대역폭 증가
. 데이터 전송률 저하
. 복잡도 증가
가. channel capacity
○ 「 채널 용량 」이라 함은, Shannon(샤논)(1948)에 의하여 다음의 공식으로 표현
C = W log₂(1 + S/N) 여기서, C : 채널용량, W : 대역폭, S :신호전력, N : 잡음전력
- 잡음이 없다면(S/N -> ∞) 임의 대역폭에서도 채널 용량을 거의 무한으로 할 수 있으나, 잡음이 있다면 대역폭을 아무리 증가시켜도 채널용량을 크게 할 수가 없다.
채널용량에 대한 Shannon의 증명은 채널 용량 C 에 도달하는 방법을 제공하는 것이 아니다.
- 즉, 『잡음이 존재하는 곳에서 신뢰할만한 통신』이라는 이론적 한계치를
* 이는 정보전달과 그 한계용량에 대한 상호관점을 제시하는 것이다.
- 한편, 채널 용량 한계치에 도달하는 방법들에 대해서는 부호화이론 등 에서 이론적 한계치 C 에 근접하기 위한 방법을 찾고 있다.
. R > C : 어떤 부호화 기술을 사용하더라도 에러 존재
. R < C : 적정한 부호화 기술 만 사용하면 오류 최소화 가능
- 이 이론은 어떤 정보소스(제공지)가 채널용량보다 작은 정보율로 보내고자 한다면 에러 또는 잡음을 없앨 수 있는 부호화(Ccoding)과정이 존재한다는 것이다.
. 달리 말하면, 정보율이 채널용량 보다 크다면 오류가 나올 확률을 피할 수 없다는 것이다.
- 이는 정보이론(Information Theory)의 기초가 되고 있다.
즉, 최적의 통신시스템 설계에 대한 이론적 근거를 제시한다.
4. Interleaver
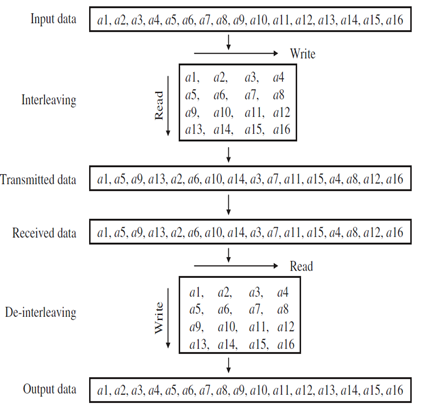

나. 홀수 짝수 인터리버
○ 짝수번째 비트는 짝수 위치로 홀수번째 비트는 홀수위치로 가도록 인터리빙을 하는 방식이다. 광 인터리버는 인터리빙 방식으로 합성 신호 스트림으로 고밀도 파장 다중분할 채널의 두 세트를 결합하는데 사용되는 3포트 광섬유 장치이다. 터보 부호에서는 일반적으로 원하는 부호율을 얻기 위하여 펑처링을 한다. 이때 주의해야 할 점은 모든 정보비트에 대해 펑처링을 한 후에 패리티 비트가 골고루 분포되어야 한다는 점이다. 예를 들어 부호율이 1/3인 경우 1개의 정보비트에 대하여 2개의 패리티 비트가 사용된다. 부호율을 1/2로 높힐 경우 2개의 패리티 비트 중 어느 한 개를 펑처링해야 하는데, 인터리빙을 잘못하면 어떤 정보비트들은 2개의 패리티 비트를 가질 것이고, 어떤 정보비트들은 패리티 비트가 모두 천공되어 패리티 비트를 하나도 가지지 않게 되어 패리티 비트가 모든 비트에 골고루 분포하지 않게 된다. 즉, 부호의 정정능력이 모든 정보비트에 대해 균일하지 않게 된다. 따라서 패리티 비트를 갖지 않는 정보비트의 경우에는 2개의 복호기 모두에서 좋지 않은 성능을 갖게 된다. 이를 위해 짝수번째 비트는 짝수위치로, 홀수번째 비트는 홀수위치로 가도록 인터리빙을 하게 되면 첫번째 구성부호에서는 짝수(홀수) 패리티를, 두번째 구성부호에서는 홀수(짝수) 패리티를 보낼 수 있게 된다. 이러한 인터리버를 Odd-even 인터리버 혹은 Mod-2 인터리버라고 한다.
○ Convolution 인터리버
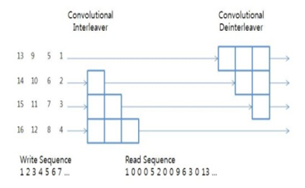 Convolution 인터리버 기본 원리(1) |
 Convolution 인터리버 기본 원리(2) |
5. Block code (Hamming code, Cyclic code, BCH code, RS code)
○ 블록 부호(block code)는 일정한 길이의 송신데이터 비트 (예를 들어 k 비트)에 r 비트의 추가비트를 삽입한다. k+r=n이라 두면 k비트의 정보를 보내기 위하여 n비트의 부호어를 보내게 된다. 베이스밴드 송수신인 경우와 달리 변조가 필요한 경우 이를 반송파에 실어 보내는 과정을 디지털 변조과정이라 한다. 수신기는 디지털 복조과정을 거쳐서 수신 부호어를 결정하고 이를 복호하여 송신 부호어를 추출한다. 제대로만 이루어지면 여기에서 k비트의 정보를 온전히 추출할 수 있다. 문제는 오류정정능력인데, 이를 크게 하고 싶으면 r이 증가해야 한다는 점다. 즉, 원하는 오류정정능력을 유지하면서 가능한 조금만 추가비트를 첨가할 수 있다면 가장 좋은 결과를 가져올 것이다.
블록 부호의 복호 방식은 부호화방식에 따라 달라지는데, 대표적으로 Hamming 부호, BCH 부호, Reed-Muller 부호, Reed-Solomon 부호 등이 있으며, 이들의 복호방식에 관한 꾸준한 발전이 이루어져 이제는 많이 실제로 사용되고 있다. BCH부호의 특별한 경우에 해당하는 Reed-Solomon부호는 deep space satellite communication modem에 길쌈부호와 연결하여 강력한 오류정정능력을 갖춘 직렬연쇄부호로 구성되어 태양계 탐사 위성체에서 각종 사진자료를 전송하는데 이용되고 있으며, 또한 compact disc에 응용되어 고전음악과 rock음악을 망라하여 충실도 높은 저장/재생에 이용되고 있다. 향후, 음악뿐만 아니라 영화 등의 영상정보와 기타 문자 데이터를 기록할 DVD등에도 이용하기 위하여 연구/개발 중에 있으며, 수신 신뢰도를 향상시키기 위하여 디지털 라디오방송과 TV방송에도 적용되어 연구/개발되고 있다. 문제는 이들의 부호화/복호화 과정을 이해하기 위해서는 꽤 복잡해 보이는 대수학적인 개념을 먼저 이해해야 한다. 그 이유는, 한 블록의 부호어를 가지고 덧셈과 뺄셈 그리고 곱셈과 나눗셈 등을 수행 가능해야 하기 때문이며, 대수학적 기초 개념은 이러한 연산이 정의되는 유한집합에 대한 개념을 이해하는 것으로부터 출발한다.
<일정 블록 단위로 구분된 코드/코딩>
블록 부호/코드 즉 고정된 코드길이를 갖는 부호 (고정길이 부호)이다. 블록 부호화/코딩은 데이터를 일정 블록 단위로 묶어서 부호화와 복호화를 수행하는 방식으로 오류정정 부호화를 위한 채널부호화 시에 많이 사용
<Block Code의 구분>
Linear Coding (선형 부호 방식)은 어떤 선형조건이 블록부호의 구조에 가해지어 선형 블록 부호가 된다. 예를 들면 Hamming Code, Hadamard Code, Golay Code 등이 있다.

Cyclic Coding (순환 부호 방식)은 선형 블록 부호의 부분 집합이다. 이는 선형성에 순환성이 추가로 가해진 구조로써 아주 단순하고도 효율적이고 쉽게 구현 가능 하며 예를 들면 BCH 부호, RS 부호, PN 코드 등이 있다.
<블록 부호화 방법>
블록 부호화 벙법에는 형태 구성 방법과 기본 부호화 방법이 있다. 형태 부호방법은 입력되는 데이터 비트들을 일정한 블록 단위의 길이로 잘라서, 이에 패리티 비트를 추가시켜 한묶음 단위(Block)로 부호화 하는 것으로써 한편, 복호시에는 데이터 및 패리티를 비교하여 살펴서 발생된 에러를 정정하게 된다.
기본 부호화 방법은 부호어들 간에 해밍 최소거리가 가능한 최대가 되도록, 유효 부호어를 2k개로 제한 선택 하는 것이다.
<블록 부호 특징>
앞뒤 블록들간의 관계가 있다. 블록 부호화는 콘볼루션 부호화와 달리, 블록들 간에 기억되는 메모리(기억성) 없다. 즉, 연속되어 발생되는 블록들 앞과 뒤 블록 간에는 아무런 관계가 없다.
구현 회로적인 특징으로는 기억소자 없이 오직 입력에 의해서 만 출력이 결정되는 조합논리회로로 구현 가능하다.
블록 부호에 대한 행렬 표현으로써의 특징은 보다 간결한 해석 도구를 제공하며, 부호기 및 복호기의 하드웨어 구현을 용이하게 한다. 또한 에러정정 능력이 커짐에 따라 복잡도가 급격하게 증가하는 경향이 있다. 블록 부호의 특징 중 장점과 활용은 콘볼루션 부호화 보다는 Burst Error에 강하여, 주로 고속 전송 방식에 많이 활용한다.
※ Burst Error = 에러가 일시적으로 연속하여 발생하고, 또 일반적으로는 에러비트 사이에 오는 교정비트의 수가 목표로 하는 수보다도 적게 되는 현상. 데이터 전송 시 한 무리의 데이터에 집단적으로 오류가 발생한 것 릴레이의 불규칙한 동작, 전송 회선의 접촉 불량, 번개, 고압선과의 간섭 등에 의해 일어난다.
가. Hamming code
○ 데이터 전송시 1 비트의 에러를 정정할 수 있는 자기 오류정정부호의 일종
○ (n,k) 선형블록부호, 순회부호의 특성을 갖음
* 미국의 Bell 연구소의 Hamming에 의해 고안된 간단한 블록부호 (1950년)

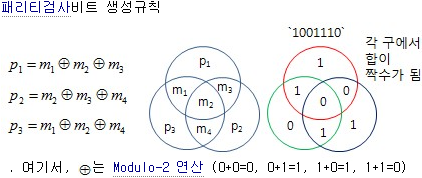
<(7,4) 해밍 부호 특징>
해밍 부호의 특징은 유효 부호어 개수가 16개이다. (2k = 24 = 16개) 닫힘특성이라고 불리는 특성은 두 부호어의 합이 다시 또다른 부호어가 되고 (7,4)의 최소 해밍거리는 3이다. 즉 임의의 두 부호어 쌍 간에 항상 3 비트 만 상이하다는 뜻이다. 신드롬 수는 8개인데, 1개는 오류가 없고 나머지 7개는 비트 오류 징후가 있다는 뜻이다. 오류검출능력 : td ≥ dmin - 1 = 3 - 1 = 2 dmin - 1 보다 작거나 같은 모든 오류 패턴을 검출할 수 있다. 오류정정능력 : tc ≥ (dmin - 1)/2 ≥ (3-1)/2 = 1 인데, 이는 잉여 패리티검사비트가 (n-k)인 3개 비트가 추가되므로, dmin의 상한이 3 이 되면서 오류정정능력 비트수는 1 비트가 된다. 각 부호의 해밍거리가 3 이상의 부호어로하는 부호계에서, 각 부호어의 거리가 3 이상이므로 하나의 부호어가 1 비트 잘못된 부호는 다른 부호어와 명확하게 구별할 수 있으므로 원리적으로 1 비트 에러를 정정할 수 있다. 패리티 비트를 필요한 수 만큼 정해진 위치에 두어서, 에러가 발생했을 때 에러 발생 비트를 알아내어 정정이 가능하도록 한다.
<해밍조건>
2 p >= m + p + 1 (m : 정보 비트 수, p : 최소잉여 비트 수)
결국, 패리티 비트 수 p 는 위 관계식에 의해 결정된다.
나. Cyclic code
○ 선형성에 순회성이 추가적으로 부과된 블록부호의 부분집합이며, 다중 비트오류에 대한 오류정정이 가능한 선형블록코드의 일종이다. 순회부호의 예는 해밍 부호, Golay 부호, BCH 부호, RS 부호, PN 코드 등이 있다.
<순회부호 성질>
순회 부호의 성질은 매우 저렴한 전자회로로 쉽게 구현 가능하다. 코드 그 자체가 구조적이고 규칙성을 갖고 있으므로, 설계구현시 선호되며, 부호화 및 신드롬 계산이 간단한 SR(시프트 레지스터)를 이용하여 쉽게 구현 가능하다 또한 직렬 구현 또한 가능하다. 효율적인 부호화/복호화가 가능한데, 순회부호에 대한 갈로아의 유한체(Galois Finite Field) 수학적 행렬 표현에 의해 아주 단순하고도 효율적인 부호화/복호화 알고리즘을 도모한다. 순회부호 조건은 선형부호 이어야 하고, 임의의 한 부호어를 순환 이동(cyclic shift)시키어도 이 역시 부호어 이어야 한다.
<(7,3) cyclic code>
 |
 |
다. BCH Code
○ BCH Code는 순회부호의 일종 으로써 연집오류 정정능력이 매우 좋으며, 다수의 오류를 정정 가능하도록 해밍부호를 일반화한 것이다. BCH란 발견자 Bose, Chaudhuri, Hocquenghem 3인의 머리글자를 딴 것이다. m을 양의 정수리 할 때, -1 또는 2 이하의 부호 길이에 대해서 mt비트의 검사 비트를 받는 것만으로 t개의 오류를 수정할 수 있다.
- BCH 주요 파라미터블록 길이 : n = 2m-1 (m = 3,4,...)패리티 검사 비트 수 : n - k ≤ m t해밍 최소거리 : dmin ≥ 2t + 1
- 1960년 Bose와 Chaudhuri는 특수한 순환부호를 소개했고 이와는 독립적으로 Hocquenghem(1959) 도 같은 순환부호를 소개했는데 이 부호를 이들의 이름을 따서 BCH 부호라한다. BCH 부호는 생성 다항식의 근들에 의하여 정의된 순환부호이며 여러개의 오류를 정정할 수 있는 부호이다. BCH 부호를 일반적으로 정의하기 전에 이중 오류정정이 가능한 길이 15인 부호를 구성할 수 있다는 것을 보이도록하자. α를 GF ( 2^4 ) 의 원시원소라 하고 근이 α, α^2, α^3, α^4 인 g(x)를 생성 다항식으로 갖는 부호 C를 생각하자. 4장에서 살펴본 GF ( 2^4 ) 의 원소들과 그 원소들의 최소다항식은 다음 표와 같다.
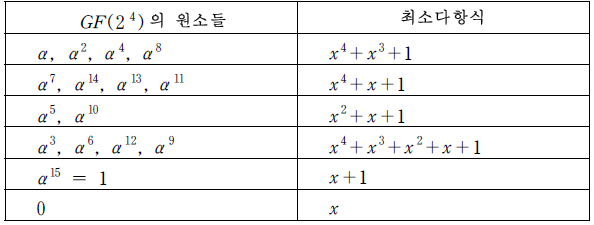
α , α^2, α^4, α^8 의 최소다항식은 x^4+x^3 + 1 이고, α^3 의 최소다항식은
x^4+x^3+x^2+x + 1 이므로 (물론 α^6, α^12, α^9 의 최소다항식도 x^4+x^3+x^2+x + 1 이다) 부호 C 의 생성다항식은 g ( x) = ( x^4+x^3 + 1 ) ( x^4+x^3+x^2+x +1 )이다. C 는 [15, 7] 부호이다. 이 부호 C 가 이중오류정정 부호인 이유를 알아보자. C 의 패리티검사행렬 H 의 임의의 4개 열이 일차독립이라면 C 가 이중오류 부호임을 안다. C 의 구성 방법에 의하여 C 의 모든 벡터는 행렬 H 의 행들과 수직임을 알 수 있다.
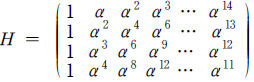
H 는 열이 15개, 행이 4 × 4 = 16 개인 이진행렬을 나타낸다. 분명히 H 의 모든 행이 독립은 아니다. 그러나 H 의 행 중에는 C 의 표준 패리티검사행렬의 행들이 존재한다. GF ( 2^4 ) 위의 행렬 H 의 임의의 4개의 열은 독립이다. 왜냐하면 이 4개의 열로 구성된 행렬의 행렬식은 한 Vandermonde 행렬식의 배수이기 때문이다. 예를 들어 H 의2번째, 3번째, 5번째, 8번째 열로 구성된 4 × 4 행렬 M 의 경우는 다음과 같다.
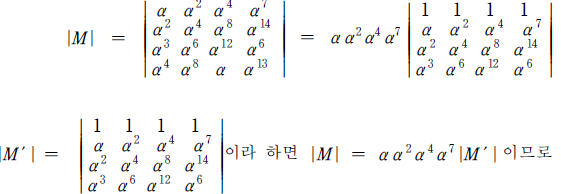
|M | = α α^2 α^4 α^7 ( α^2 - α ) ( α^4 - α ) ( α^4 - α^2 ) ( α^7 - α ) ( α^7 - α^2 ) ( α^7 - α^4 )이고 α 가 GF (2^4) 의 원시원소이기 때문에 |M | =/ 0 이다. H 의 임의의 4개열이 GF ( 2^4 ) 위에서 독립이기 때문에 당연히 GF ( 2 ) 위에서 독립이고 따라서 C 의 최소무게는 5 이상이고 C 는 이중오류정정부호이다. 이것을 3장에서 구성한 이중오류정정부호로 생각할 수 있지만 이제부터 임의의 오류 개수를 정정할 수 있는 순환부호를 구성하는 방법에 대하여 생각해 보자.
gcd ( n, q ) = 1 일 때 C 를 GF ( q ) 위에서 길이 n 인 순환부호라 하자. m을 mod n 에 관한 q 의 위수라 하자.
즉 m = min {k | q k ≡ 1 ( mod n ), k 는 자연수 }라하자 α 를GF ( q^m ) 에서1의 원시n 제곱근 이라하자.
부호C 의 생성다항식 g ( x ) 가δ -1 개의 연이은 원소 α^b, α^b + 1, …, α^b + δ - 2 의 서로 다른 최소다항식들의 곱일 때 이 부호를 의도거리designed distance) δ 인 BCH 부호라 한다.
<갈로아 필드(Galois Field)>
간단히 말하면 체(field)란 사칙연산을 자유롭게 할 수 있는 수체계라고 정의할 수 있는데 이 중에서 원소가 유한인 것만을 생각합니다. 가장 기본적인 것으로는 어떤 소수(prime number) p에 대해서 0, 1, 2, ... , p-1 으로 이루어진 집합을 생각할 수 있습니다. 이 수들의 연산은 일반 자연수의 연산처럼 한 후에 p로 나눈 나머지를 취하는 것입니다. 이런 유한체들을 Z_p 라고 씁니다.
(p는 첨자) 전산과에서 많이 쓰는 부울리언 대수는 Z_2 에 해당합니다.어떤 체가 있으면 우리는 그 체의 확장체(extension field)를 생각할 수 있습니다.
확장체란 원래의 체에 새로운 원소들을 추가해서 여전히 체가 되도록 만든 것이라고 생각할 수 있습니다. 예를 들자면 유리수와 실수, 실수와 복소수가 이런 확장체의 경우에 해당합니다.
이런 확장체를 만들 때 가장 자연스럽고 기본적인 방법은 다항식을 생각해서 그 근을 추가하는 것입니다.
실수에서 x^2 +1 = 0 이라는 다항식을 생각하면 실수에서는 근이 없기 때문에 허수 i를 추가하게 되고 복소수라는 확장체를 얻습니다.
이제부터는 몇가지 알려진 사실만을 간략하게 쓰겠습니다.
사실1. 어떤 체가 있고 그 체의 원소들을 계수로 갖는 다항식을 생각했을 때 그 다항식의 근을 모두 포함하는 확장체를 만들 수 있다.
사실2. 어떤 유한체가 있을 때 그 유한체는 어떤 소수 p에 대해서 Z_p의 확장체(extension field)이고 이 때 p는 유일하게 결정된다.
다시 말하면 어떤 유한체이든 Z_p 에 몇 개의 원소들을 추가해서 여전히 체가 되도록 만든 것입니다.
사실3. 어떤 유한체도 어떤 소수 p와 자연수 n에 대해서 Z_p의 원소들에 다항식 x^(p^n} - x 의 근들만을 추가한 Z_p의 확장체이다. (위 다항식의 차수는 p^n) 그리고 원소의 총 개수는 p^n 개다.
따라서 GF(2^8)이란 부울리언 대수 Z_2에 다항식 x^(2^8) - x 의 근들을 추가한 확장체이고 원소의 개수는 2^8 = 256 개인 유한체입니다.
다. RS Code
○ 1961년 I.S.Reed 와 G.S.Solomon이 제안한 비 2진 순환부호로써, 오류정정 능력이 우수할 뿐 만 아니라 통신로 상에서 발생하는 랜덤 오류(Random Error) 및 연집 오류(Burst Error)까지 모두 정정할 수 있다는 장점 때문에 각종 디지털 시스템상에서 광범위하게 사용되고 있는 채널부호화 방식이다. <특징>연집 에러(Burst Error)에 강하다.(페이딩 채널에서 좋다) 예를들어 Compact Disc, DAT(Digital Audio Tape), 유선 통신 등에서 많이 사용되며, 이동통신 등에서는 RS 부호 보다는 콘볼루션 부호화 방식인 터보 코드가 많이 사용된다. 에러 정정 능력에 따라 복잡도는 선형적 또는 지수적 증가 하며 에러 정정 능력 이상의 에러는 수정 불가하다. 10-7 이상의 에러율에서 좋은 성능을 가지며 고속 전송이 가능 (수백 Mbps)하고 비트 단위가 아닌 심볼 단위로 부호화한다.
<RS(n,k) 심볼 부호 조건>
(n,k) = (2m-1,2m-1-2t)
- 0 < k < n < 2m+2
- k : 메세지 심볼 수
- n : 부호 심볼 수
- t : 부호 심볼 오류정정능력
- m : 심볼 길이(m 비트열)
Reed Solomon 부호는 RS(n, k)의 형태로 표시를 하는데 이는 k개의 입력 데이터 심볼에 오류 수정을 위한 parity 심볼을 더하여 n개의 심볼을 출력한다는 의미 이다.
즉 n-k 개의 parity가 데이터에 추가된다. 이렇게 parity데이터가 추가되어 데이터가 커지는 단점이 있지만 오류가 발생한 경우 이를 이용해 완벽하게 정정할 수 있다.
Reed Solomon부호의 오류 정정 능력은 parity부호의 양과 관련이 있는데, 다음 식을 만족하는 t개의 심벌을 수정할 수 있다.
2t = n – k 예를 들어 1byte가 1개의 심벌을 이룬다고 가정하고, 188 bytes MPEG 2 Transport Stream (TS)에 적용되는 RS(204,188)코드의 경우를 보면 188개의 심벌 데이터에 16개의 심벌 parity가 추가되어 204개의 심벌로 구성된 codeword를 출력하게 된다.
이때 이 코드의 오류수정 능력은 2t = 16 이므로 t = 8, 즉 최대 8개의 심벌 오류를 수정할 수 있다. 만약 1개의 심벌에 1bit씩 오류가 발생했다고 가정을 하면 RS(204,188)코드는 최대 8비트 오류만을 수정할 수 있고, 1개의 심벌에 6bit의 오류가 발생하는 경우 RS(204,188)코드는 6*8 =48 bit의 오류를 수정할 수 있다.
따라서 오류가 여러 개의 심벌에 걸쳐서 발생하는 경우보다는 연속적은 오류(Burst error)에 대해 보다 장점이 있다고 할 수 있다.

6. Convolutional code, Turbo code, LDPC
가. Convolutional code
○ 컨볼루션 코드(길쌈 부호화)는 오류정정부호의 일종으로써, 블록 부호화기와는 달리 길쌈 부호화기는 메모리(기억성)를 갖고 있다. 즉 부호화때 현재의 입력 신호에 과거의 일부 신호를 함께 활용 (비 대수적 구조)하며, 블록부호화는 해당 블록에만 의존하나, 길쌈부호화는 그 이전의 블록에도 의존한다. 이를 칭하는 다른 말로는 돌림형 부호, 콘볼루션 부호 라고도 한다. 길쌈은 꼬여 펼쳐진 나무 형상을 상징하며, 전송되는 전후 비트들 간에 인위적으로 상관관계를 형성하여 줌으로써 어느 한 비트에서 오류가 발생하더라도 전후에 수신된 다른 비트들의 패턴을 이용하여 오류를 추정할 수 있다.
<길쌈부호의 응용>
길쌈 부호의 주요 용도는 CDMA 이동통신 등 무선통신 환경에 널리 사용된다. 무선채널 상에서 산발적으로 나타나는 오류(Scattered Error)들에 대한 오류정정 능력이 우수하기 때문이다. 하지만가우시안 채널에서는 좋으나, 반면에 연집 에러(Burst Error)에는 약하다. 음성급 영역과 같이 다소 저속의 데이터율의 경우에 주로 사용된다.Viterbi Code의 경우 IS-95 등에서 이용되며, Turbo Code는 IMT2000 등에서 이용된다.
<구현>
시프트 레지스터(Shift Register) 및 Modulo-2 덧셈기로 구현 가능
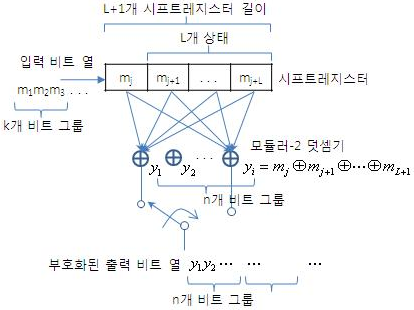
- 현재와 과거 L개의 상태들에 의해 영향 받음
- (n,k,L) 부호화기
. k : 원 메세지 비트 열 길이
. n : 부호화된 비트 열 길이
. L : 상태 수, 부호기 메모리(기억성) 길이
- 구속장 : n(L+1)
. 과거의 영향을 받는 비트 열 길이
<복호화>
길쌈부호의 복호는 거의 대부분 연판정 비터비 복호 알고리즘을 이용한다. 이는 최대 유사도 (Maximum Likelihood) 복호화를 할 수 있는 효율적인 기법이다. 한편, 구속장 길이가 10을 초과하면 순차 복호화를 사용한다.
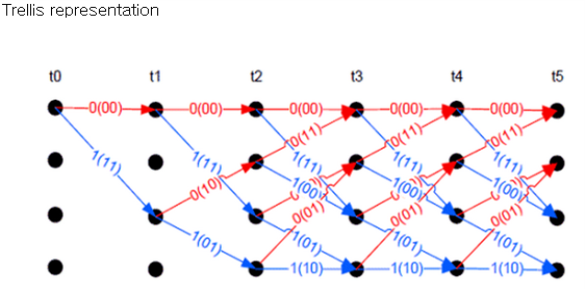
`길쌈 부호화기를 특징짓는 주요 요소로써, 구속장, 코드율, 입력 비트 수, 출력 비트수 등 이 있고, 길쌈 부호의 표현 방법으로는 다항식 이용, 상태 다이어그램 또는 트렐리스 다이어그램, 행렬 표현 등이 있다.
구속장의 증가에 따른 복잡성이 지수적으로 증가 한다. 특히, (구속장 > 9) 인 경우, 복호기의 구현이 어렵다. 따라서, 실제 구현시에는 구속장 길이가 10 보다 크지 않도록 한다. 특징으로는 다항식을 이용하여 쉽게 표현될 수 있으며, 행렬 형태로 나타낼 수 있다. 또한 상태 다이어그램이나 트렐리스 다이어그램으로 나타낼 수 있다.
* 길쌈부호의 종류
- 비시스템적 길쌈부호 (non-systematic convolution code)
- 시스템적 길쌈부호 (systematic convolution code)
- 쳐드 길쌈부호 (punctured convolution code)
나. Turbo code
○ 터보부호는 기본적으로 길쌈 부호(convolutional code)를 병렬 연접하는 방식이다. 이것은 두 개 이상의 구성 부호화기(component code)에 같은 시퀀스의 서로 다른 배열을 적용하는 것이다. 즉 원래 연구되어 오던 직렬 연접 부호가 전송하고자 하는 시퀀스에 하나의 부호를 적용하여 부호화한 다음 이 부호화된 시퀀스에 다른 부호를 적용하여 다시 부호화하는 이중 부호화의 과정이었다던 것에 비해 새로 제안된 터보 부호는 같은 시퀀스를 배열만 바꿔서 서로 다른 부호화기에 적용하는 방법이다. 차세대 이동 통신 시스템에서는 고속의 멀티미디어 데이터의 신뢰성 있는 전송을 요구하며 고속 데이터의 신뢰성을 높이기 위해서는 강력한 채널 코딩 및 효율적인 변조 방식이 요구된다. 이동 통신의 결정판이라고 할 수 있는 IMT-2000(International Mobile Telecommunications-2000)은 현재 각 국가별로 개별적으로 운영되고 있는 다양한 이동전화 시스템의 규격을 통일, 세계 어느 곳에서도 동일한 단말기로 서비스를 이용할 수 있도록 하는 차세대 이동 통신 시스템으로서, ITU를 중심으로 2Mbps급 고속 데이터통신이 가능한 사양 등을 갖추도록 제안되고 있으며 그 규격에 따라 각 국에서 도입이 진행되고 있다. 터보 코드는 최근 ITU 등에서 IMT-2000 등 차세대 이동 통신에서 고속 데이터 전송용으로 채널 코드의 표준으로 채택된 상태이다.
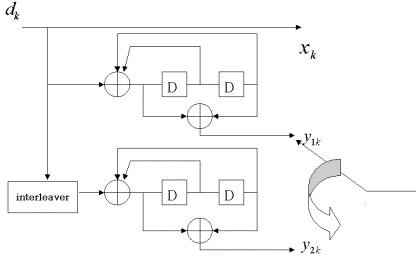
<터보 부호화기>
터부 부호의 부호화기는 일반적으로 아래 그림1과 같이 길쌈 부호화기 두개와 이 두개의 부호화기를 연결하는 인터리버로 이루어져 있다. 입력 시퀀스 d는 첫 번째 구성 부호화기 를 통해서 부호화하지 않은 출력 Xk와 부호화된 출력 Y1k를 발생시킨다. 같은 입력 시퀀스 dk 는 인터리버를 통과한 후 두 번째 구성 부호화기를 통과하여 부호화된 출력 를 통과하여 부호화된 출력 Y2k를 발생시키게 된다. 이러한 터보 부호의 부호화 방법은 지금까지 많이 적용되어 온 직력 연접 부화처럼 한 부호화기를 통과한 시퀀스에 다른 부호호기를 적용 한다기 보다는 두개의 부호화기가 비록 배열은 다르지만 같은 입력 시퀀스의 집합에 적용된다는 점 때문에 이를 병렬 연접 부호 (parallel concatenated code)라고 부른다.
<터보 복호화기>
터보 부호에서는 복호화 방법으로 각각의 비트에 대하여 정보를 발생시킬 수 있도록 MAP 알고리즘을 이용한다.

또한 복호의 성능을 향상시키기 위하여 반복복호를 이용한다. 그림 2는 반복 복호를 적용한 기본적인 터보 부호의 복호화기를 나타내고 있다. 그림에서 볼 수 있는 것과 같이 각각의 MAP 복호화기는 정보비트와 잉여 비트, 부가 비트 (extrinsic bit) 를 입력으로 받아 들어서 각 비트에 대한 로그 상관 함수 (Log likelihood Ratio)를 출력으로 발생시킨다. 이 LLR 을 구성하고 있는 부가 정보는 다음 복호화기 단의 사전 정보 (Priori Information)가 되어 복호의 신뢰도를 향상시키게 된다.
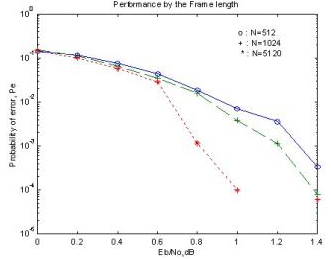
<터보코드 시뮬레이션 결과>
 |
 |
○ 시뮬레이션은 프레임의 길이에 변화를 주었을 때 성능을 비교한 그림이다. 구성부호기는 메모리는 2개의 생성다항식이 인 것을 사용하였으며, 부호율은 1/2로 펑처링을 하였다. 랜덤인터리버를 사용하고 인터리버의 크기는 N= 512, 1024, 4096으로 하였으며, BPSK 변조와 AWGN 채널을 가정하였고, Log-MAP 알고리즘을 이용하여 반복 복호 회수는 max=6으로 하였다. 프레임의 크기가 커질수록 성능이 좋아짐을 알 수 있다.
시뮬레이션은 프레임을 고정하고 반복 복호수의 변화에 따른 성능을 비교한 그림이다. 구성부호기는 메모리는 2개의 생성다항식이 인 것을 사용하였으며, 부호율은 1/2로 펑처링을 하였다. 랜덤인터리버를 사용하고 인터리버의 크기는 N= 5120으로 하였으며, BPSK 변조와 AWGN 채널을 가정하였고, Log-MAP 알고리즘을 이용하여 반복 복호 회수는 1회에서 6회로 변화를 주었다. 반복 회수가 늘어남에 따라 성능이 좋아짐을 알 수 있다.
<개요>
* 인코더를 각기 다른 인터리빙에 두 개 이상 연결하여 큰 Coding gain을 얻어내는 기술.
* 1993년도에 Berrou[1]에 의해 제안
* Code rate를 1/2로 했을 경우 Eb/No가 0.7인 환경에서 Bit error
* Probability가 10 -5 까지 떨어지는 획기적인 성능 가짐.
* 터보 코드의 에러정정 능력은 충분히 큰 인터리빙에서 시뮬레이션을 통해 연구되어졌고, 샤논에 의해 정립된 이론적인 한계에 가장 근접 채널상에서 발생하는 오류를 정정하기 위하여 사용되는방식
*장점 : 눈에 띄는 BER성능의 향상
*단점: 디코더의 구성시 복잡한 회로구성과 시간지연이 발생
<작동>
구성 : 일반적으로 인터리버에 의해 분리된 2개의 코드로 만들어진 인코더를 이용. 인코더는 일반적으로 규칙적으로 순환하는 콘볼루션 코드(RSC 코드) 로 구성.
동작 : 인터리버에 의해서 분리된 두 개의 인코더는 서로 다른 입력 시퀀스에 의해
동작하게 되고, 그리하여 두 개의 분리된 디코더를 필요로 함.
다. LDPC
○ 차세대 통신시스템에서 요구하는 고속 데이터 전송을 가능하게 하는 강력한 오류정정부호이다. 특징으로는 부호의 길이를 크게 함에 따라 비트당 오류 정정 능력이 향상된다. 반면 비트당 계산 복잡도는 그대로 유지되는 LDPC 반복 복호 기번의 특성에 기인하다. 그리고 병렬적으로 복호 연산을 수행할 수 있도록 부호의 설계가 가능하므로 긴 부호의 복호를 고속으로 처리할 수 있다. ETSI DVB-S2/C2/T2등의 디지털 방송 시스템과 IEEE 802.3an등의 대용량 이더넷의 표준들에 채택되었다. 터보 코드와 비교를 하면 복잡성은 LDPC가 복잡하지만, 처리속도는 LDPC가 빠르다. 터보코드는 WCDMA나 LTE에 적용되어 활용하고 LDPC는 802.16e/m에 적용된다. 시스템 적용면에서는 복잡도가 낮고 H-ARQ등의 지원이 가능한 터보가 유리하고 데이터 처리속도 면에서는 LDPC가 유리하다.
- LDPC는 부호는 등가의 이분 그래프(biparite graph)표현인 Tanner 그래프로 자주 나타낸다.
- Tanner그래프는 H를 입사 행렬로 하는 그래프이고 H의 각 열들을 변수 노드로 각 행들은 체크 노드로 하고 H의 각 1들은 하나의 변수 노드와 하나의 체크 노드를 연결하는 에지를 의미한다.
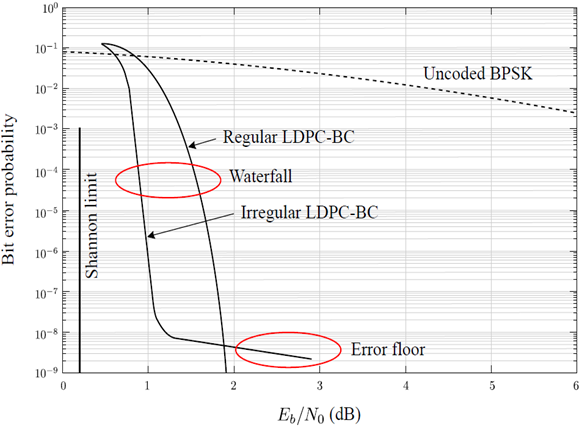
- 모든 변수 노드의 차수가 동일하고 모든 체크 노드의 차수가 동일한 경우는 Regular LDPC이고 위 경우가 아닌 경우는 Irregular LDPC이다. 아래는 Regular와 Irregular의 BER 성능 차이이다.
○ LDPC부호를 효율적으로 부호화하기 위해서는 Richardson에 의해 제안된 부호화 방법을 이용한다.
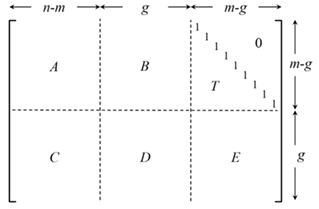 |
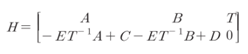 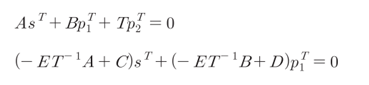 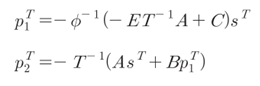 |
- Raptor Like LDPC

○ LDPC부호의 복호
저밀도 특성과 반복 복호 기법의 특성으로 인해 복호 복잡도가 부호 길이에 비례한다. 최적이고 가장 많이 사용하는 복호 기법은 message-passing 반복 복호 기법이다.
* message-passing
1. 채널에서 수신한 정보를 바탕으로 Tanner 그래프 상에서 노드들이 서로 메시지를 주고받으며 원래의 부호어를 확률적을 추론하는 일련의 과정
2. 사이클이 없는 그래프 상에서 유도된 메시지 전달 알고리즘을 유한한 길이의 LDPC 부호에 그대로 적용하더라도 충분히 좋은 결과를 얻을 수 있다는 것이 험적으로 검증.(실제 시스템에서 이용)
* belief propagation 복호 기법
1. 수신 값이 연판정 데이터인경우에 적용
2. 로그 우도 비율 사용(log likelihood ratio, LLR)
3. 𝑝 j = 해당 메시지와 연관된 변수 노드의 송신 값이 j ( j= -1, 1 )일 확률

○ Girth가 많으면 BER 성능이 우수하다, 하지만 복잡도는 증가한다. 주로 6,8을 사용한다.
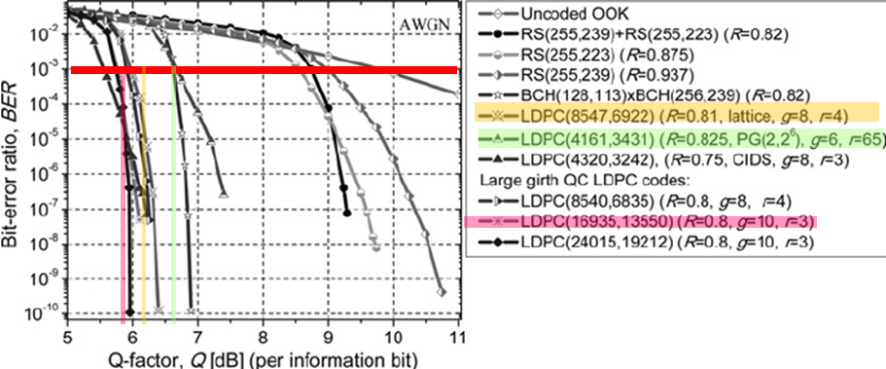

라. AMC(Adaptive Modulation&Coding)
○ 무선 채널에서 수신전력, 페이딩, 혼신 등 전파 상태에 따라 수시로 변조 및 코딩 방식의 파라미터를 변경하여 최대의 데이터 속도를 얻도록 하는 기술
- Adaptive multimedia modulation technique
- Adaptive turbo code modulation
- BER technique
기지국에서 가까울수록 차수가 높은 modulation을 사용하기 때문에 기지국과 가까울수록 euclidean distance가 가까워 BER 성능은 떨어지게 됨으로써 BER 성능 개선을 위해 더 효율이 좋은 channel coding을 사용함으로써 BER을 개선하게 된다. 따라서 환경에 따라 다르게 사용할 수 있지만 일반적 이론으로는 기지국과 가까운 순서로 LDPC, TURBO, Convolution code를 사용하여 통신환경을 최적으로 맞추게 된다.
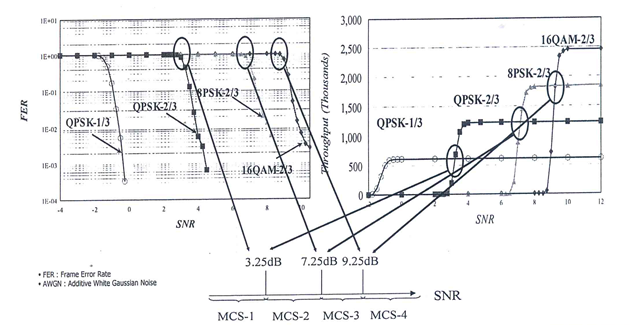
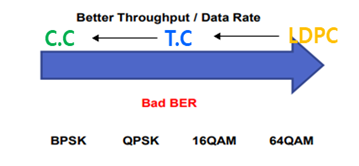 [ Modulation 차수와 BER 비교 (1) ] |
 [ Modulation 차수와 BER 비교 (2) ] |
7. Application System
가. GSM
○ Source coding
* Sampling rate : 8000 samples/sec
* 1 frame length : 160 samples, 20ms
* 1 sub-frame : 40 samples, 5ms ( 1 frame = 4 sub-frame)
* Input : 13bit uniform PCM signal ( PSTN의 8bit A-law companded PCM format
신호는 13bit uniform PCM format으로 바꾸어 주어야 함 )
* Output : 260bit parameters / frame(20ms), 260bit*1/20ms = 13Kbps data rate
Short term filter parameter(LPC analysis) : 36bits/20ms
Long term filter parameter(LTP analysis) : 9bits/5ms(36bits/20ms)
RPE parameter : 13 pulses regular excitation signal/sub-frame,
(3bit APCM coding per each pulses)
2bit grid position/sub-frame,
6bit block amplitude/sub-frame
13*3+2+6=47bits/sub-frame
47bits/5ms(188bits/20ms)
=>36+36+188=260bits/20ms
*LPC analysis : filter order p = 8, frame마다 필터파라메터(reflection coefficient)를 계산 reflection coefficient(-1≤R.C≤1)는 LARs(log area ratios)값으로 바꾸어 6bit부터 3bit까지 부여. (6*2+5*2+4*2+3*2=36bits)
*LTP analysis : sub-frame 단위로 LTP lag와 LTP gain을 계산
LTP lag(value : 40~120, 7bits), LTP gain(value : 1~3, 2bits)
*RPE encoding : sub-frame단위로 long term residual의 입력을 받아 4개의 pulse set를 생성하고 그 중 최적의 cadidate를 택한다(2bits).
그리고 선택된 candidate의 pulse 중 최대갑의 절대값(6bit,by log)을 전송하고 13개 펄스의 크기를 APCM(Adaptive Pulse code modulation)방법으로 코딩하여 전송한다(13*3=39bits).
*4분가량의 음성을 RPE-LTP로 녹음시 필요한 메모리 용량
160 샘플(20ms) - (RPE-LTP) -> 260bit
∴ 4분 데이터 => 260*50*60*4 = 3,120,000bit
보코더는 20ms 동안의 데이터를 한꺼번에 분석.
125Ms 간격으로 160회의 관측이 이루어지므로 총 160개의 13비트짜리 데이터에 대해서 분석압축을 위해 이전의 여러 시간대에서 20ms동안의 데이터 세트들을 가지고 있는데 보코더는 현재 얻은 20ms동안의 데이터를 가진 이전의 시간대를 찾아낸다.
현재의 데이터와 선택된 이전 시간대에서의 데이터의 차이를 구한 후 이 차이에 대한 데이터를 260비트로 출력한다.
보코더는 20ms의 시간대마다 260비트만의 데이터를 출력, 음성신호의 자기상관관계 이용 160*13=2080비트 정보를 260비트의 정보로 압축한 것 , 1sec에는 20ms시간대가 50개 있으므로 보코더의 출력은 초당 260*50=13000비트 즉 13kbps가 된다.
○ Channel coding
음성 데이터는 두 단계로 채널 코딩한다.
*Block-coding
이것은 cyclic code이고 단순히 error를 검출을 위하여 사용된다. 3개의 parity bit를 음성 데이터에 더한다. 만약 디코더에서 Type Ia bis에서의 error가 검출되면 동일 block 속에 들어 있는 260개 bit 전부가 음성 codec으로 보내어지지 않고 버려진다. Codec에서 복원하는 것보다 더 좋은 음성 품질을 보장한다.
*Convolutional coding
이것은 여분의 bits를 Type Ia bits와 Type Ib bits에 더하여 디코더가 error를 검출하고 바로 잡을 수 있도록 해준다. convolutional code에서 rate는 r=1/2이고 delay는 K=5이다. 이것은 redundancy bits를 계산하기 위하여 5개의 연속하는 bit들이 사용된다는 것을 의미하는데 각각의 data bit에 부가적인 redundant bit가 더해진다. GSM에서는 적당한 redundancy bits를 계산하기 위하여 연속하는 5개의 bit들을 사용하기 때문에 data bit의 뒤에 zero값을 가지는 4개의 bit를 더한다.

나. IS-95
○ Source coding
*QCELP(Qualcomm Code Excited Linear prediction)
IS-95의 표준인 부호 분할 다중 접속(CDMA) 방식 디지털 이동 통신 시스템의 음성 부호화 방식으로 미국 퀄컴 제안으로 CDMA 음성 부호화기는 음성의 속도와 음량에 따라 전송 속도가 가변된다. 즉, 빨리 말할 때는 높은 음성 부호화율, 말이 없을 때는 낮은 부호화율을 적용하여 개인의 채널 사용량을 절약하며, 비교적 낮은 전송률에서도 우수한 음질을 내는 반면에 복잡한 계산량이 요구된다.
○ Channel coding
*Convolutional Code
- Forward Channel -
순방향채널에서는 부호율이 1/2이고 구속장이 9인 컨벌루션코드가 사용된다.

- Reverse Channel -
역방향채널에서는 채널이 열악한 상태에 있어 부호율이 1/3이고 구속장이 9인 성능이 우수한 컨벌루션 코드가 채택되어 사용되고 있다.

○ 1개의 비트 스트림이 입력되면 shift register의 지연 및 비트 덧셈 동작에 의하여 2개의 비트 스트림이 출력되거나, 3개의 비트 스트림이 출력되게 한다. 인코더에 의하여 redundancy 비트가 늘어날수록 코딩율은 낮아지고 에러에 대한 강인성은 증가하지만, redundancy 비트에 의하여 무선구간에서의 전송 효율, 즉 사용자 전송속도는 감소하게 된다. 산발적인 에러에 강한 특성을 갖는 컨벌루셔널 채널코딩에 있어서 최대 몇 비트까지 연속된 비트 에러를 복원할 수 있는가는 전적으로 구속장의 길이에(쉬프트 레지스터의 개수) 의하여 결정이 된다.
다. CDMA 2000
○ Source Coding
* LD-CELP
저속의 이동 통신을 위해 16kbps로 부호화하면서도 동등이상의 음질을 얻을 수 있다. 이 기술을 이용한 음성 부호화의 표준이며, 1992년 ITU-T에 의해 권고 되었다. 인간의 청각 특성을 고려, 음성신호의 5샘플을 1프레임으로 하는 10바이트만 전송함으로써 부호화 지연 2ms내에서 높은 음질을 구현한다.
* CS-ACELP
8kbps로 ADPCM보다 음질이 좋다.
○ Channel Coding
FCH 및 DCCH에서의 컨벌루션 코드 사용으로 고성능을 제공할 수 있으며, 터보 코드의 사용으로 SCH에서의 고속 데이터 전송 성능을 향상 시킬 수 있다.
라. UMTS
○ Source coding
AMR(Adaptive Multi-Rate)는 음성 코덱으로 무선 접속망의 제어에 따라 4.75, 5.15, 5.9, 6.7, 7.4, 7.95, 10.2, 12.2kbps 등 8가지 중에서 1가지를 선택하여 음성을 부호화하여 전송한다. 비트 오류가 많은 환경에서는 채널 부호화에 많은 비트를 할당하여 많은 비트 정정이 가능하도록 하고 비트 오류가 적은 환경에서는 음성 압축기에 많은 비트를 할당하여 음성 압축 성능을 향상시킨다.
VP(Video Phone Service)는 VP서비스는 CS(Circuit Switched)도메인 H.324를 사용하며, 그것은 비디오 코덱, 오디오 코덱, 데이터 프로토콜, 멀티플렉스 등으로 구성되어 있다.
○ Channel coding
DownLink
- Convolutional coding with rate 1/2: Yi = 2*Ki + 16;
rate 1/3: Yi = 3*Ki + 24;
- Turbo coding with rate 1/3: Yi = 3*Ki + 12.
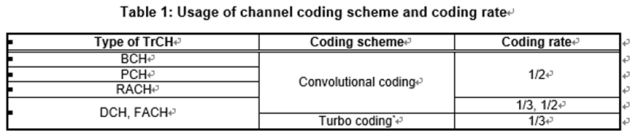
- Convolutional coding
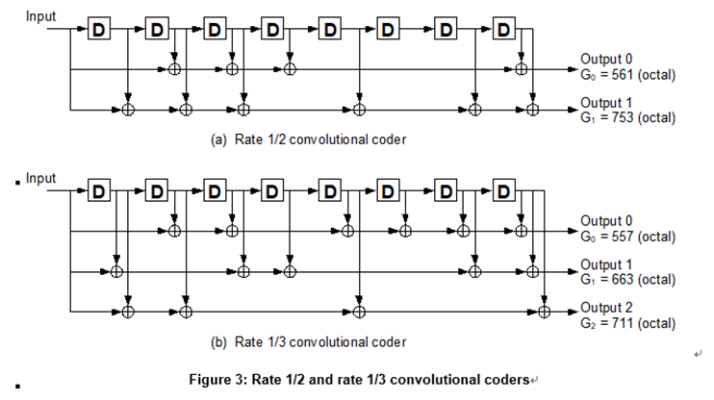
마. LTE
Channel coding_[TS 36.212]
- TrCH에 따라서 coding scheme와 coding rate 결정

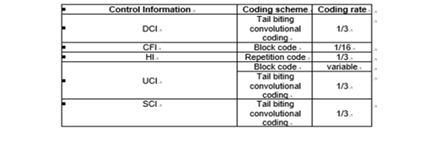

바. NR(5G)
○ CRC calculation
1. Input bits to the CRCcomputation : a0,...,a(A-1)(A: size of the input sequence)
2. Parity bits : p1,...,p(L-1) (L: number of parity bits)
3. The bits after CRC attachment : b0,...,b(B-1)
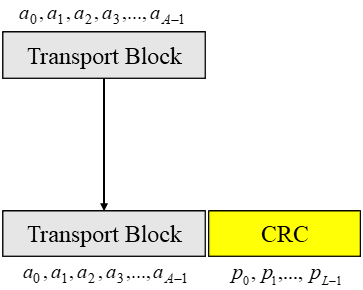
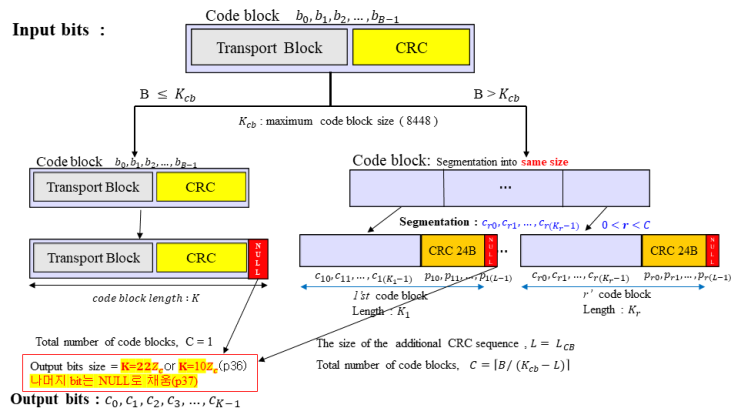
○ Low density parity check coding
1. The input bit sequence to the code block segmentatino is denoted by b_0,...,b_(B-1) where B>0
2. If B is larger than the maximum code block size Kcb, segmentation of the input bit sequence is performed and an additional CRC sequence of L = 24 bits is attached to each code block.
3. For LDPC base graph 1, the maximum code block size is Kcb: 8448
4. For LDPC base graph 2, the maximum code block size is Kcb: 3840
8. Reference & Acronyms
- AMR(Adaptive Multi-Rate)
- ARQ(Automatic Repeat Request)
- BEC(Backward error correction)
- BER(Bit error rate)
- CDMA (Code Division Multiple Access)
- CS(Circuit Switched)
- CS-ACELP(Conjugate Structure Algebraic Code Linear- Prediction)
- DCCH(Dedicated Control Channel)
- FEC(Forward error correction)
- LDPC(Low-density parity-check code)
- LD-CELP(Low Delay Code Linear Prediction)
- QCELP(Qualcomm Code Excited Linear prediction)
- RPE-LTP ( Regular Pulse Excited – Long Term Prediction )
- RSC(Reed-Solomon code)
○ Web site
http://blog.naver.com/PostView.nhn?blogId=mcokbody&logNo=20014729382
http://coding.yonsei.ac.kr/hm/index.html
http://blog.naver.com/greatworld?Redirect=Log&logNo=100007943741
○ BOOK
Introduction to Wireless and Mobile Systems, Second Edition
쉽게 설명한 3G/4G 이동통신 시스템
IMT2000 CDMA 기술
IMT Advanced&B4G Core Technology Contents((3GPP TS 36.211 V10.4.0)
Digital Communications: Fundamentals and Applications , Second Edition
'컴퓨터 과학 및 기술 연구 > 통신공학이론' 카테고리의 다른 글
| "이동통신시스템의 핵심 기술" 이론 정리 6편( OFDM & OFDMA & SC-FDMA) (3) | 2024.01.30 |
|---|---|
| "이동통신시스템의 핵심 기술" 이론 정리 5편(MIMO Diversity & MIMO Multiplexing) (0) | 2024.01.29 |
| "이동통신시스템의 핵심 기술" 이론 정리 3편(Modulation / Demodulation) (2) | 2024.01.27 |
| "이동통신시스템의 핵심 기술" 이론 정리 1편(Multiple Access) (1) | 2024.01.26 |
| "광통신시스템의 핵심을 알면 세상이 바뀐다" 기초 이론 정리편 (1) | 2024.01.25 |
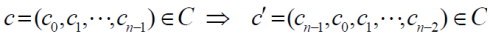


댓글