1. GAN의 후속 연구들
○ goodfellow에 의해 GAN이라는 architecture가 제시된 이후, GAN은 여러가지 분야로 응용되기도 했고 앞서 말한 문제점들을 해결하기 위한 여러가지 시도가 있었다. 아래 이미지를 통해 GAN의 후속연구들을 볼 수 있다.

2. Conditional GAN
○ 2014년 Mehdi Mirza, Simon Osindero 에 의해 제안된 GAN의 변종 알고리즘이다.
○ 때때로 이미지를 처음부터 생성하기보다 이미 있는 이미지를 다른 영역의 이미지로 변형하고 싶은 경우가 많다. 예를 들어, 스케치에 채색하거나, 흑백 사진을 컬러로 만들거나, 낮 사진을 밤 사진으로 바꾸고 싶을 때 등이다.‘cGAN(Conditional GAN)’은 이를 가능케 해주는 모델이다.
○ 기존의 GAN의 생성자가 랜덤 벡터를 입력으로 받는 것에 비해 cGAN의 생성자는 변형할 이미지를 입력으로 받는다. 그 뒤 생성자는 입력 이미지에 맞는 변형된 이미지를 출력한다. 예를 들어 스케치 사진을 받은 생성자는 그 스케치에 맞는 색을 칠한 뒤 채색된 이미지를 출력하는 것이다. 구분자는 스케치와 채색된 이미지를 모두 보고 그 채색된 이미지가 과연 스케치에 어울리는지 판단한다. 구분자를 속이기 위해서 생성자는 첫째, 진짜 같은 이미지를 만들어야 하고 둘째, 스케치에 맞는 이미지를 만들어야 한다.
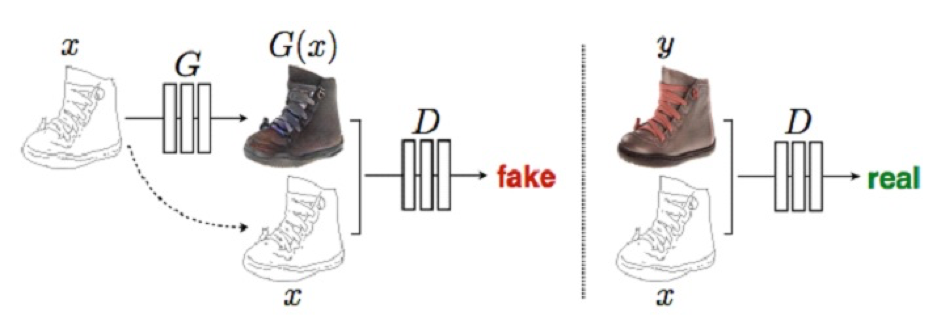
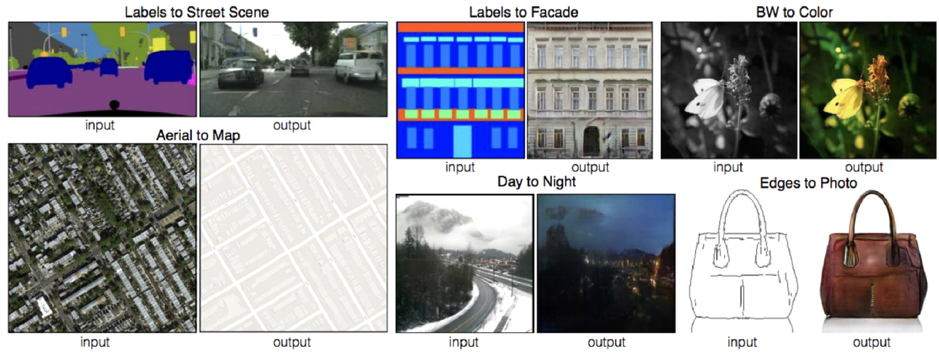
○ cGAN의 혁신은 주어진 이미지를 새로운 이미지로 변형하는 수많은 문제를 하나의 간단한 네트워크 구조로 모두 풀었다는 점이다. 모든 문제는 이미지에서 의미적인 정보를 찾아내어 다른 이미지로 바꾸는 문제로 볼 수 있기 때문이다. 이렇게 한 영역의 이미지를 다른 영역의 이미지로 변형하는 문제의 경우 cGAN이 유용하게 쓰일 수 있다.
○ Generator과 Discriminator에 추가 정보 y를 condition으로 제공해 줄 수 있는 GAN이다. 이 때 추가 정보 y는 class label이 될 수도 있고, 다른 modal data가 될 수도 있다. 예를 들어, MNIST dataset의 경우 각 숫자의 종류를 y로 주어, 원하는 종류의 숫자를 생성하도록 조건으로 줄 수 있다.
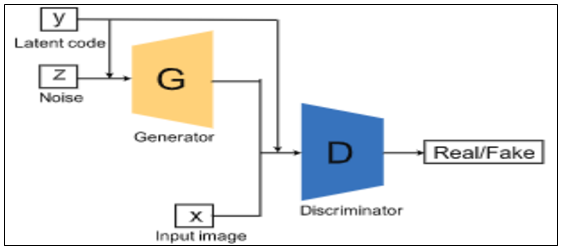
○ CGAN은 기본 GAN 모델의 생성자와 판별자에게 초기 정보 x이외에 추가 정보 y를 주어 주어진 조건에맞는 결과를 생성하도록 유도한 기법이다. 생성자를 훈련할 시에 추가 정보 y가 조건으로 작용하여 새로운 정보를 획득할 수 있으며 원하는 결과로 유도할 수 있다. CGAN의 판별식은 아래와 같이 구성된다.

○ 즉 한마디로 정리해보면, GAN 학습과정에서 y라는 condition 변수를 추가함으로써 자신이 원하는 label의 데이터를 생산해낼 수 있도록 만든 GAN 모델. 이라고 보면 된다.
3. Wasserstein GAN
○ GAN의 가장 큰 문제점 중 하나는 불안정한 학습(unstable train)이다. GAN은 parameter에 대하여 데이터 분포를 실제 데이터의 분포와 비슷하게 만드는 것(maximize loglikelihood)이 목표이다. 라벨이 따로 없기 때문에 unsupervised learning의 일종이다. WGAN에서는 아래와 같은 차별점을 통해 언급된 GAN의 문제점들을 해결하고자 한다.
- Discriminator를 critic이라 명명한다. critic은 더이상 classifier(진짜와 가짜를 구분하는)가 아니다.
- critic은 Lipschitz 조건을 만족해야 한다.
- critic은 이제 EM distance로부터 도출해낸 특정 scalar 값이 된다.
- KL divergence는 continuous하지 않은 특징 등 때문에 학습이 불안정하다.
○ Total Variation (TV)
- 두 확률측도(Probability measure, 확률분포와 동일한 의미로 받아들여도 무방)의 측정값이 벌어질 수 있는 값 중 가장 큰 값(또는 supremum).
만약 두 확률분포의 확률밀도함수가 서로 겹치지 않는다면 TV는 1이다.


- 위 확률분포들을 가우시안(Gaussian) 분포로 가정하고, 평균을 0부터 35까지로 제한한 후 p와 몇 개의 q를 시각화해보면 아래와 같다.
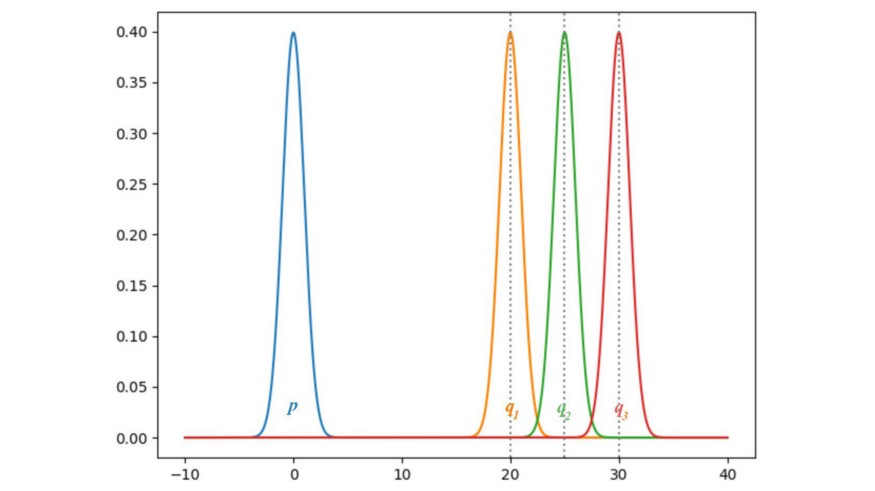
- 만약 p와 q가 동일하다면, KL-Divergence와 JS-Divergence는 모두 0이 된다. 하지만 q의 평균이 점차 커질수록, 두 경우 모두 Divergency의 gradient가 0에 가까워진다. 이 경우, Generator가 gradient descent 방식으로 학습을 진행해도 진전이 없게 된다.

- WGAN은 Vanishing Gradient 문제 해결을 위해 Wasserstein Distance에 기반한 새로운 cost function을 도입한다. 아래는 그 비교 결과이다.

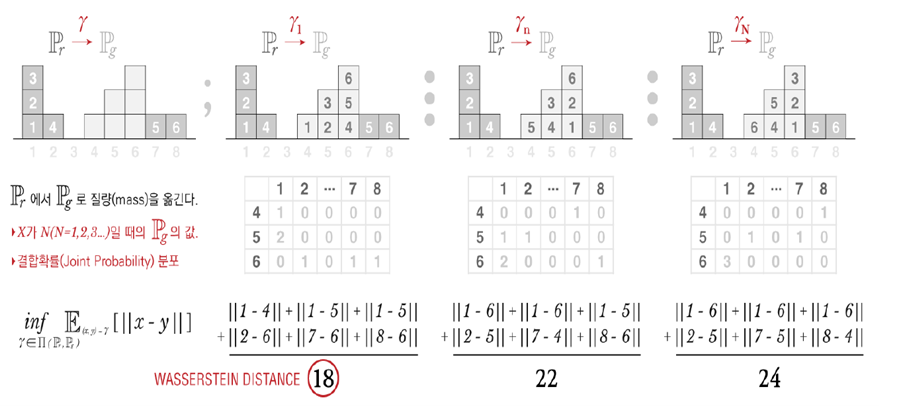
○ Earth-Mover(EM) Distance(=Wasserstein-1)
- 두 확률분포의 모든 결합확률분포(joint distribution) Π(P,Q) 중에서 d(X,Y)의 기댓값을 가장 작게 추정한 값
- Wasserstein Distance는 두 확률 분포간의 사이를 측정하는 방법이다. Earth Mover’s Distance라고도 불려서, 줄여서 EM distance라고한다. 왜냐하면, 한 분포에서 다른 분포의 모양을 닮기 위해 옮겨지는 모래더미의 최소 비용이라고 해석되어진다. 비용은 “옮겨진 모래의 양”X”이동거리”로 계산된다.
4. Least Squares GAN
○ GAN에서는 discriminator에 sigmoid cross entropy loss 함수를 사용한다. 즉, discriminator는 자신이 받은 sample이 진짜인지 가짜인지를 구별해서 받은 sample이 "진짜"일 확률을 내보내게 된다. 문제는 이 loss 함수 때문에 generator up
date시 vanishing gradient 현상이 일어난다는 점이다.

- 그림을 보시면 sigmoid cross entropy loss 함수를 사용할 때 decision boundary와 진짜(o), 가짜(+) sample들이 있다. decision boundary를 기준으로 아래를 진짜 위를 가짜로 구별한다고 생각할 때, 별표로 표시된 가짜 sample들은 이미 진짜로 클래스가 구별되어있는 것을 볼 수 있다. 이 경우, generator 입장에서는 이미 discriminator를 매우 잘 속이고 있기 때문에 딱히 더 학습할 의지가 없습니다(vanishing gradient). 하지만 이렇게 생성한 별표 sample들을 보시면 실제 진짜 sample들이 모여 있는 분포에서는 멀리 떨어져 있게 된다.
- 이 부분을 해결하고 별표 sample들을 진짜 data 방향으로 끌고 와보자는게 이 논문의 핵심 아이디어다. 방법도 상당히 단순하고 직관적인데 매우 효과적이다.
Discriminator에 sigmoid cross entropy loss 대신 least square loss를 사용해서 decision boundary에서 멀리 있는 sample들에게 penalty를 주자는 것이다. 결국 이 부분 하나 때문에 sample이 좀 더 real data에 가깝게 나오도록 generator를 학습할 수 있게 된다.

- Least square decision boundary를 사용하면 저렇게 멀리 떨어져 있는 녀석들을 decision boundary 쪽으로 끌어올 수 있게 된다. 마치 분포간의 거리를 divergence가 아닌 least square error로 계산하는 것으로 생각할 수 있다.
- Decision boundary가 true data distribution을 지나도록 그린 이유는 사실 간단하다. 제대로 학습된 GAN의 discriminator에서 나온 decision boundary라면 진짜 data distribution을 지나게 되어있기 때문이다.
- LSGAN이 WGAN처럼 regular GAN에 비해 stable한데 특성상 discriminator가 optimal에 가까워야해서 여러번 update 해줘야하는 WGAN보다는 학습이 훨씬 빠르다.
○ 간단히 위의 아이디어를 수식으로 정리해보면 다음과 같다. 결국 기존의 GAN은 아래와 같은 minimax problem을 푸는 반면;
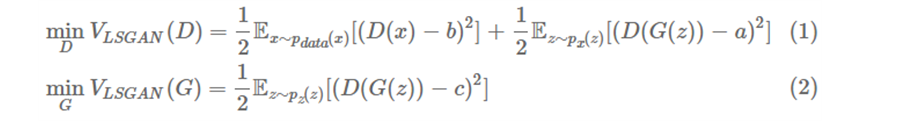
여기서 b는 real label a는 fake label c는 G 입장에서 D가 믿도록 하고 싶은 값이다.
LS이기 때문에 첫번째 식이 최소화 되려면 (.)2 안쪽이 모두 0이 되어야한다. 따라서 D(x)→b일 수록 그리고 D(G(z))→a일수록 값이 작아진다. 즉, D 입장에서는 label이 모두 맞게 잘 분류해야 잘 학습하는 것이니 수식과 하고자 하는 바가 잘 맞다. G도 비슷하게 생각하실 수 있겠다.
이 글의 내용 및 그림, 사진 등의 콘텐츠는 작성자에게 저작권이 있습니다.
이를 무단으로 복제, 수정, 배포하는 행위는 불법이며, 관련 법률에 의해 엄격하게 제재될 수 있습니다.
작성자의 동의 없이 이 콘텐츠를 사용하는 경우, 민사 및 형사상의 책임을 물을 수 있습니다.
Copyright. 우리의인공지능항해 All rights reserved.
'인공지능(LLM 구축) > AI 및 ML 알고리즘 소개' 카테고리의 다른 글
| Deep Learning 인공지능(AI) 시대 CPU의 발전 방향은? (2) | 2024.01.23 |
|---|---|
| GAN의 한계와 극복 전략: 전문가의 시선으로 살펴보는 최신 연구 동향과 해결 방법 (0) | 2024.01.22 |
| GAN 모델의 전문적인 증명 분석 (0) | 2024.01.22 |
| GAN 동작 원리(How to work) (2) | 2024.01.21 |
| Generative Adversarial Network (GAN) 개념 (2) | 2024.01.21 |


댓글